Binary Decision Tree: Analysis
Here is the schematic representation of a binary decision tree.
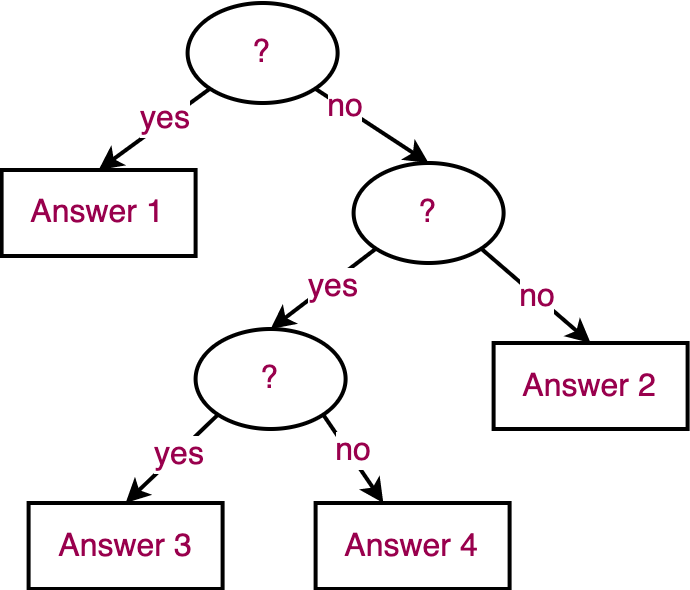
Notice the followings:
-
The decision tree is a binary tree (the answer to comparison operation is either "yes" or "no").
-
Internal nodes are binary decisions (corresponding to comparisons).
-
External nodes (leaves) are resulting outputs (answers).
-
An execution of the algorithm corresponds to a path from the root to a leaf.
-
The length of such an execution path is the running time of the algorithm for the case of the input that led to that execution.
-
The height of the tree is the worst case running time of the algorithm (i.e. the longest execution path).
Since the decision tree is a binary tree, its height is at least $\lg N$ where $N$ is the number of nodes (which is not necessarily the same as e.g. the length of the input sequence). Therefore, the lower bound on any comparison-based algorithm modeled by this decision tree is $\Omega(\lg N)$.
But what is $N$?
For searching, $N$ is $O(n)$ where $n$ is the number of elements in the search space (size of the collection).
Why?
For lower bound analysis, we consider what is the most number of nodes we can pack in a binary tree of the minimum height. This is the case in a perfect binary tree. Recall: in such a binary tree with $m$ nodes, there are $\left \lceil m/2 \right \rceil$ leaves and $\left \lfloor m/2 \right \rfloor$ non-leaf nodes (internal nodes and a root).
In the decision tree corresponding to comparison-based searching algorithm, the number of leaves is greater or equal to the number of possible answers which is greater or equal to $n$, the number of elements.
To check this claim, see the previous exercise, the number of possible outcome is $4$, one per $a_i$ plus
null.
So, if there are at least $n$ leaves, there are at least $2n$ nodes. The height of the tree therefore is at least $\lg (2n)$.
Therefore, the lower bound on any comparison-based searching algorithm is $\Omega(\lg n)$ where $n$ is the size of the search space. In other words, binary search is optimal!