In a complete binary tree, there are $\left \lceil n/2 \right \rceil$ leaves and $\left \lfloor n/2 \right \rfloor$ non-leaf nodes (internal nodes and a root).

Let's build an intuition for this. The complete binary tree can be seen as the structure of a single-elimination tournament with $k$ teams corresponding to the leaves. As a simplifying condition, imagine $k$ is even. Therefore, we have a perfect (complete & full) binary tree:

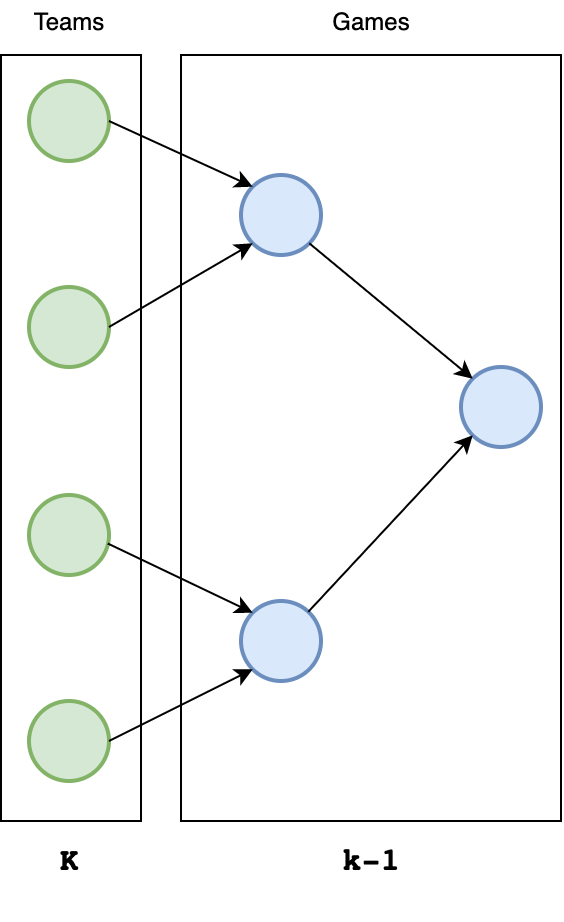
Each non-leaf (internal node) is a game in which the loser is eliminated and the winner goes up to the next round. There is one final match, which corresponds to the root.

Since there will be only one winner, there must be $(k-1)$ games (non-leaf nodes) since every other $(k-1)$ team loses exactly once. Therefore, we have $k+(k-1)=2k−1$ nodes altogether. And, we can verify that

$$ \left \lceil \frac{n}{2} \right \rceil = \left \lceil \frac{2k-1}{2} \right \rceil = k \; \; \text{leaves} $$

A similar analogy can be made for the case where $k$ is not an even number. You can imagine one lucky team rests in the first round of the tournaments and directly goes to the next round. Eventually, $k-1$ teams must be eliminated and that takes $k-1$ games (non-leaf nodes).

Aside: the "proper" approach to prove the aforementioned formula for the number of leaves is through Mathematical induction.

The implication of this observation is to simplify the implementation of the heapify process:

private static void heapify(Integer[] data) {
  for (int i = numNodes / 2; i >= 1; i--) {
    sink(data, i);
  }
}