Task 2

Consider the following graph, which represents some of the courses a CS student typically takes in their first year of study. As it can be seen, vertices are courses. A directed edge from vertex $v$ to $u$ indicates course-v is a pre-requisite of course-u.

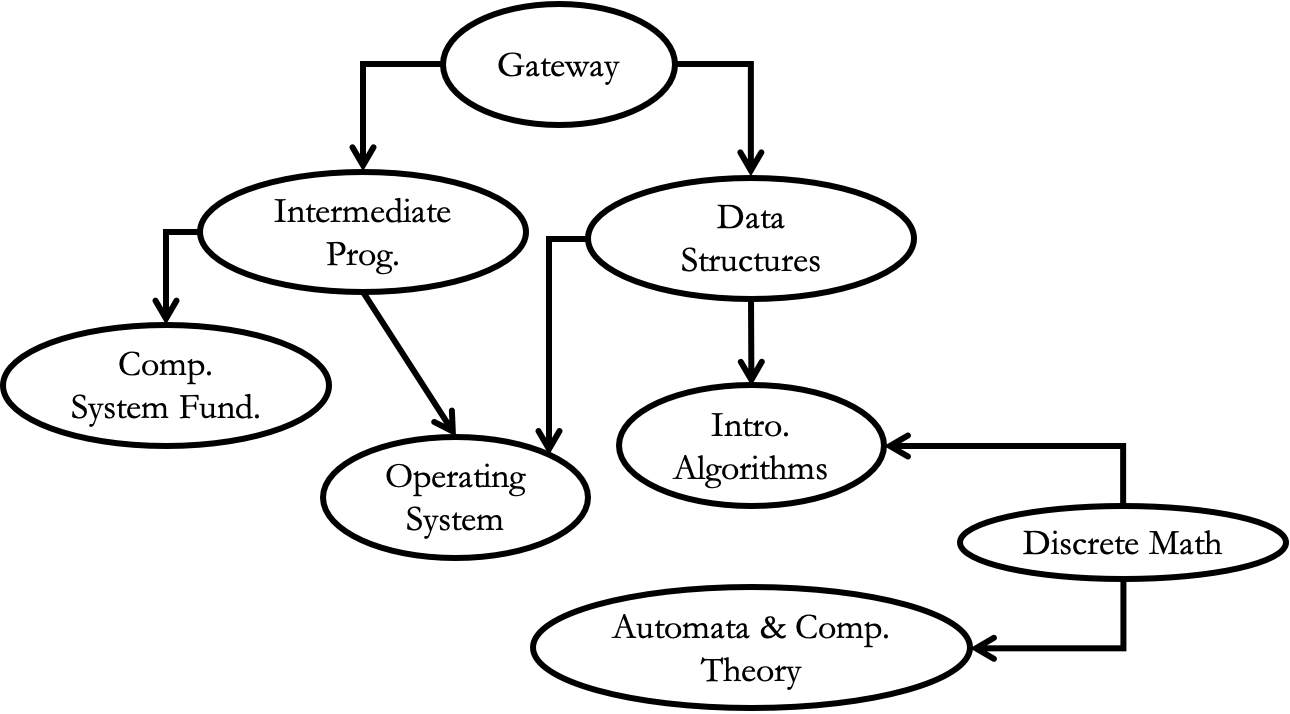
There are several different orders in which one can take these courses (the order is important since a pre-requisite must be taken before you can continue with the next sequential class).

Gateway, Intermediate Prog., Cmp. System Fund., Data Structures, Operating System, Discrete Math, Intro. Algorithms, Automata & Comp. Theory
Gateway, Data Structures, Intermediate Prog., Comp. System Fund., Operating System, Discrete Math, Automata & Comp. Theory, Intro. Algorithms
Gateway, Discrete Math, Intermediate Prog., Data Structures, Automata & Comp. Theory, Comp. System Fund., Intro. Algorithms, Operating System
Discrete Math, Gateway, Data Structures, Automata & Comp. Theory, Intro. Algorithms, Intermediate Prog.,  Comp. System Fund., Operating System
And several more!

While all the above are valid ordering of the courses, the following, for instance, is not because "Operating Systems" cannot be taken before "Data Structures."

Gateway, Intermediate Prog., Cmp. System Fund., Operating System, Discrete Math, Automata & Comp. Theory, Data Structures, Intro. Algorithms 

So, of many ways to "order" the vertices, some are "valid," and some are not. Let's reiterate this point by considering a simpler graph:

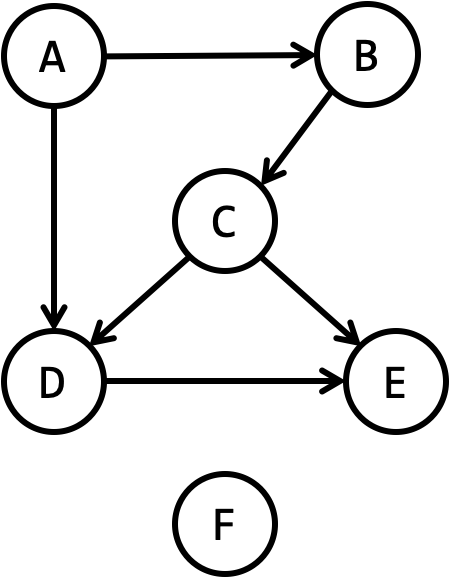
A valid ordering of the vertices of this graph is one in which all the arrows go from left to right!

An invalid ordering is one where some arrows go from right to left!

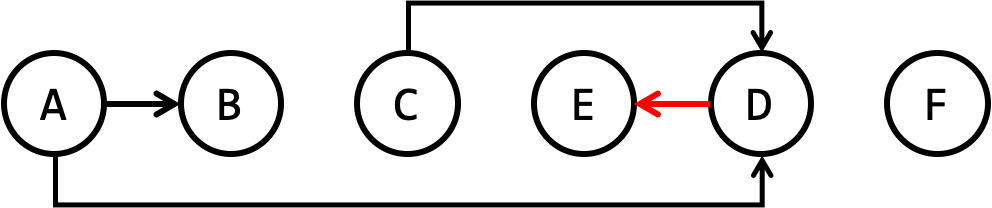
You might be wondering how we can write a program to do this ordering for us! The following demo represents an algorithm that allows you to print out a valid ordering of the vertices for any directed graph. (Assume the graph has no directed cycle in it, that is, there is no circular dependency in the curriculum!)

Your task is to implement this algorithm!

To implement the algorithm presented in the demo, you don't actually need to delete the nodes. Instead, keep track of the in-degree values and set them to $-1$ when a node is to be considered as "deleted."

Here is a pseudo-code that captures the algorithm in the demo, with the aforementioned adjustment:

Compute and store each vertex's in-degree
While there are vertices with in-degree > -1:
    find a vertex with in-degree zero and output it
    decrement in-degree of all vertices adjacent to it      
    mark this vertex "deleted" (set its in-degree to -1)

You must complete the implementation of Task2.order. A few test cases are provided in Task2Test.java file. You are encouraged but not required to add more tests. Note (1) the "valid" order is not necessarily unique. (2) When you print the vertices, you must print each vertex on a new line (see the example in Task2.order which prints all vertices in numerical order).

In your implementation of Task2.order you must follow the pseudocode provided above. A vastly different solution from the provided pseudocode will be flagged as potentially taken from unauthorized resources over the internet.

In the README file, elaborate on the running time of the algorithm provided here. Copy the pseudocode and use asymptotic notation to indicate the runtime of each line of pseudocode. Then, indicate the total running time. Finally, explain if/how you can modify the algorithm to improve its runtime. You are not asked to implement a more efficient solution; only elaborate in your README how it can be done.