Growth Factor

Consider a dynamic array based implementation of Stack. The amortized cost of push depends on the growth factor employed to expand (resize) the array.

Exercise If the array size starts at $1$, how expensive will it be to grow to $1$ million if we grow the array one element at a time?

Solution

When we call grow in the push method, if we grow the array by one (or few) elements, then the number of times we call "grow" linearly increases with the number of time we call "push".

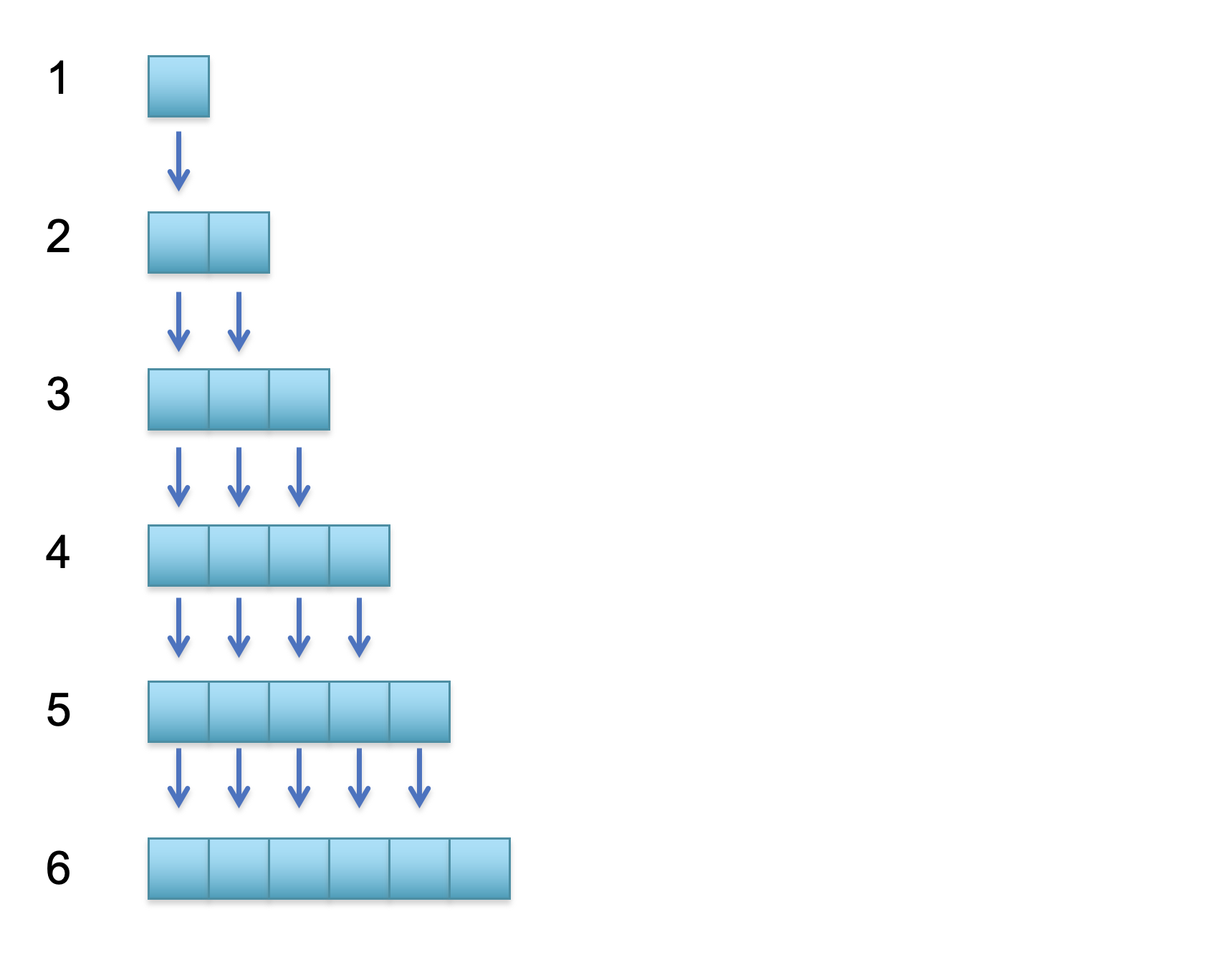
The function grow itself is a linear time operation. So we have a situation that looks like $O(n) \times O(n)$ which gives us $O(n^2)$ quadratic runtime for $n$ "push" operations.

Another way to see this is that for one million push, the work "grow" performs (in total) will be

$$ 1 + 2 + \dots + 999999 = 499999500000 \approxeq \text{1 billion} $$

which means $O(n^2)$ total runtime for $n$ "push" operations.

The amortized cost of push will then be $\frac{O(n^2)}{n}=O(n)$.

Exercise If the array size starts at $1$, how expensive will it be to grow to $1$ million if we double the size of the array each time we reach its capacity?

Solution

If we grow the array by doubling its size, the number of times we call grow logarithmically increases with the number of pushes.

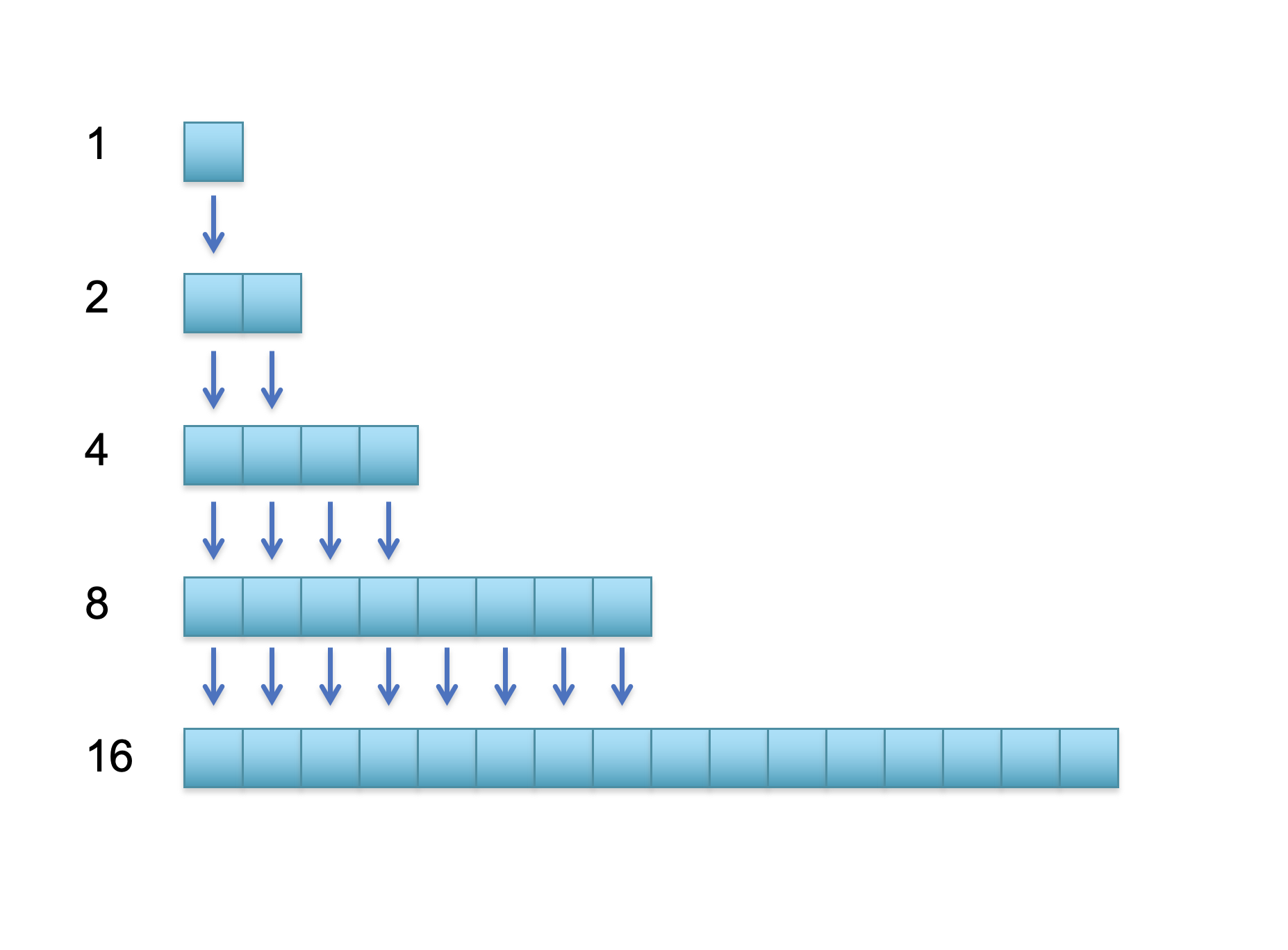
Let's say we start with an array of 1 element and then we do $n$ push, the total work done is

$$ 1 + 2 + 4 + 8 + \dots + 2^{\lg n} = 2^{(\lg n) + 1} - 1 $$

I got the total above by adding up all the powers of two.

Note that $2^{\lg n} = n$ (recall $\lg n$ is $\log_{2} n$ and look at rule #7 of logarithm rules). So we have

$$ 2^{(\lg n) + 1} - 1 = \left ( 2^{(\lg n)} \times 2 \right ) - 1 = 2n - 1 \in O(n) $$

Thus the total run time is $O(n)$ for $n$ "push" operations. The amortized cost of push will then be $\frac{O(n)}{n}=O(1)$.

To avoid incurring the cost of resizing many times, dynamic arrays resize by a multiplicative factor, such as doubling in size, so as $n$ elements are inserted, the capacities form a geometric progression.

Resources