Types of Edge
Consider this graph:
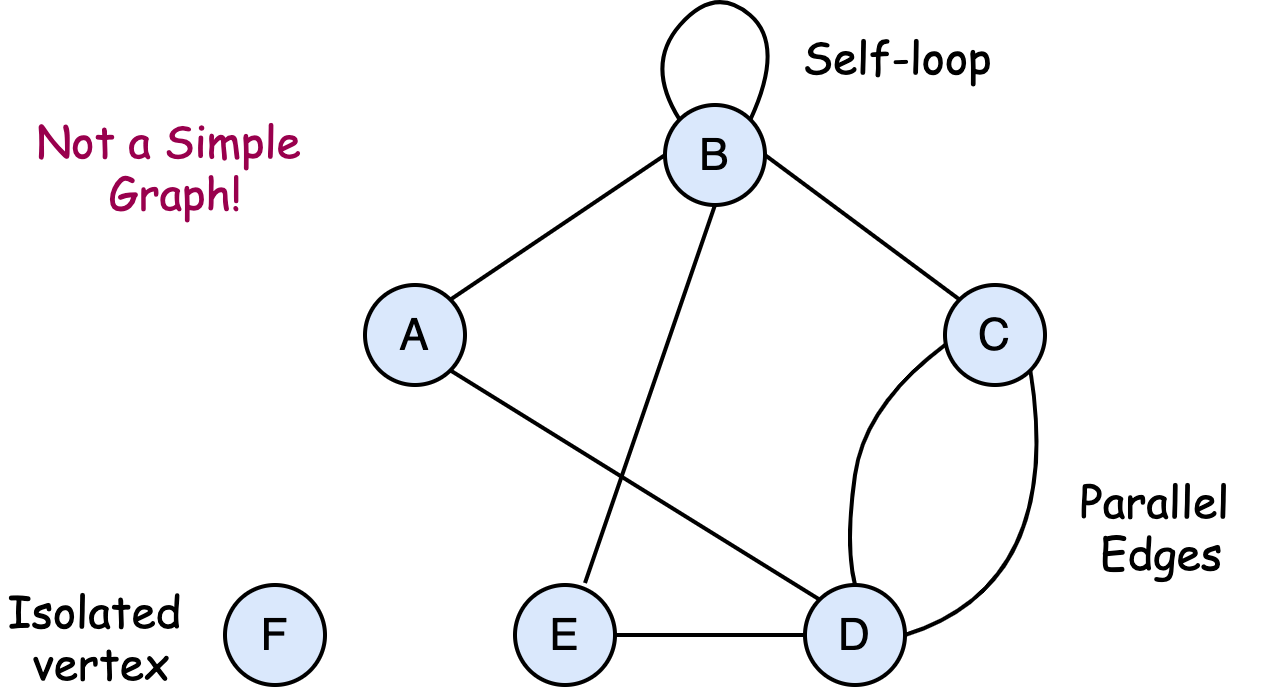
An edge can attach a vertex to itself (like $\{ B,B \}$); this is called a loop. A graph that contains loops is called a pseudo-graph.
There can be multiple edges (a.k.a parallel edges) between the same end-points (like $\{C,D \}$, which is a double edge). Graphs that have parallel edges are called multigraph.
A simple graph is one where there are no loop or multiple edges.
Exercise What kind of a graph is this?
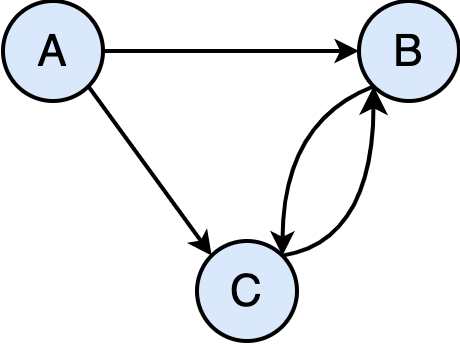
A) Directed multigraph
B) Directed pseudo-graph
C) Simple directed graph
D) Simple undirected graph
Solution
A simple directed graph.
The edges between $C$ and $B$ are directed (opposite direction) so it is not multiple-edge; thus not a multi-graph.
Aside: Not every vertex has to have an edge attached to it. A vertex with no edges is called an isolated vertex.
A graph that has an isolated vertex is not "connected".
In a connected graph, it is possible to get from every vertex in the graph to every other vertex in the graph through a series of edges.