Double Rotation: Right-Left

Consider inserting the values $3, 7, 5$ in that order.

We start by inserting $3$:

We have a BST with a single node; it is balanced!

Next, we insert $7$.

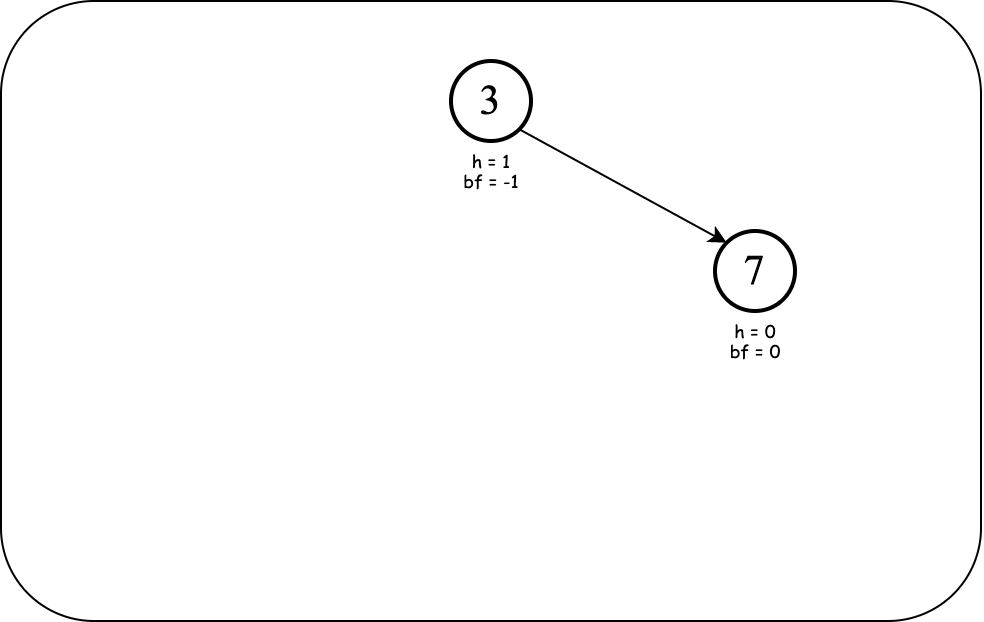
Now our BST has two nodes. Notice the height and balance factor of the root has changed (and it is still balanced).

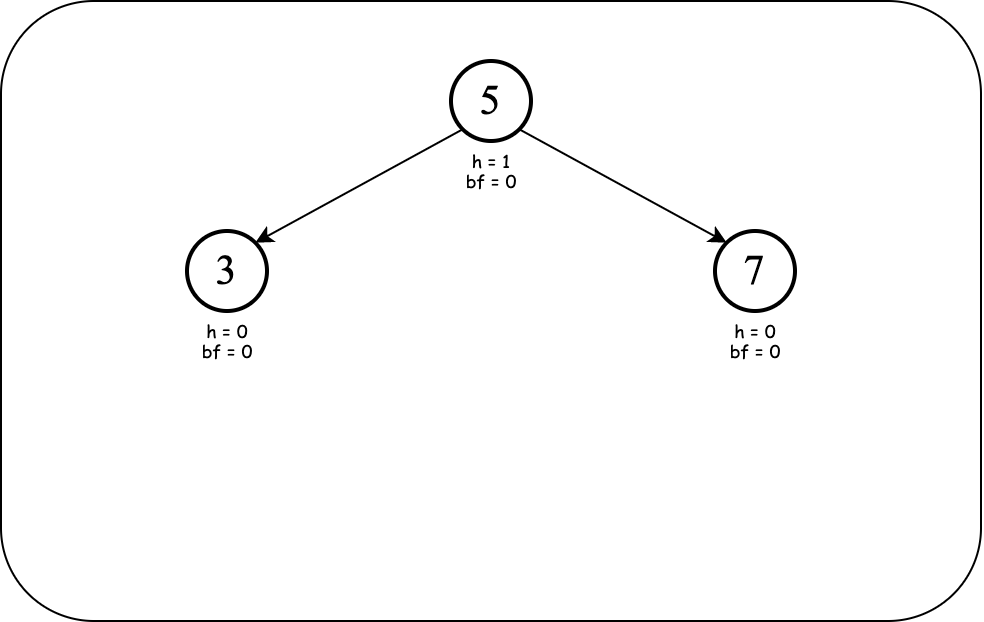
Next, we insert $5$.

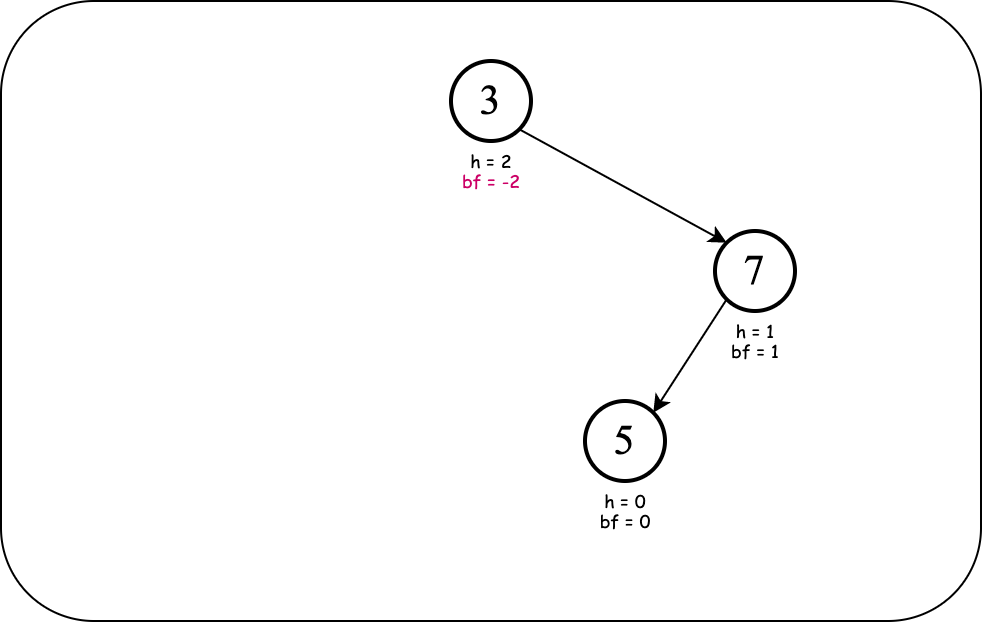
Our BST has three nodes now. Notice the heights and balance factors of the parent and grand parent of $5$ have changed. In particular, the grand parent (the root) is not balanced anymore!

However, if we were to push $7$ to the right of $5$, we would transform the structure to a pattern we have seen before:

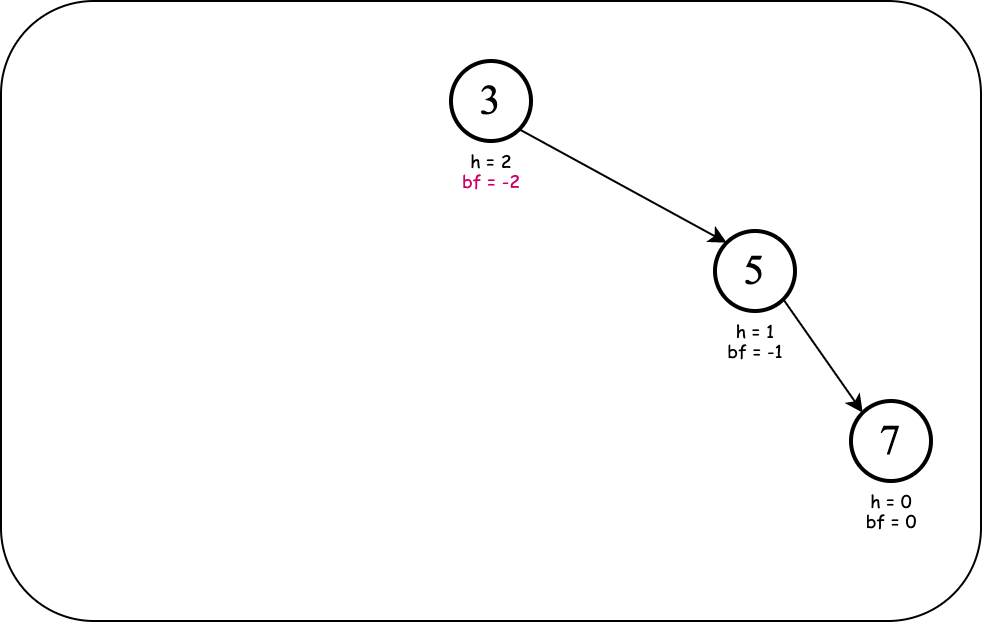
The above arrangement is a (single) left rotation away from balance

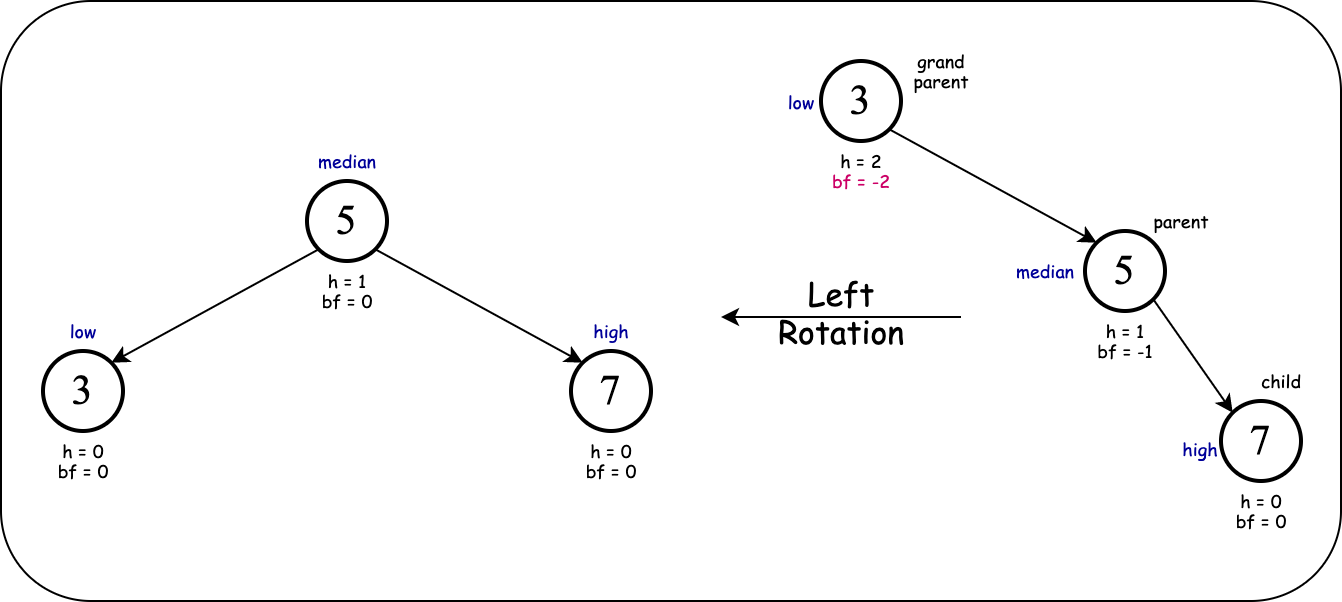
So we perform a left rotation:

As you have noticed, we needed two rotations, first a right and then a left rotation. This is called a (double) right-left rotation.

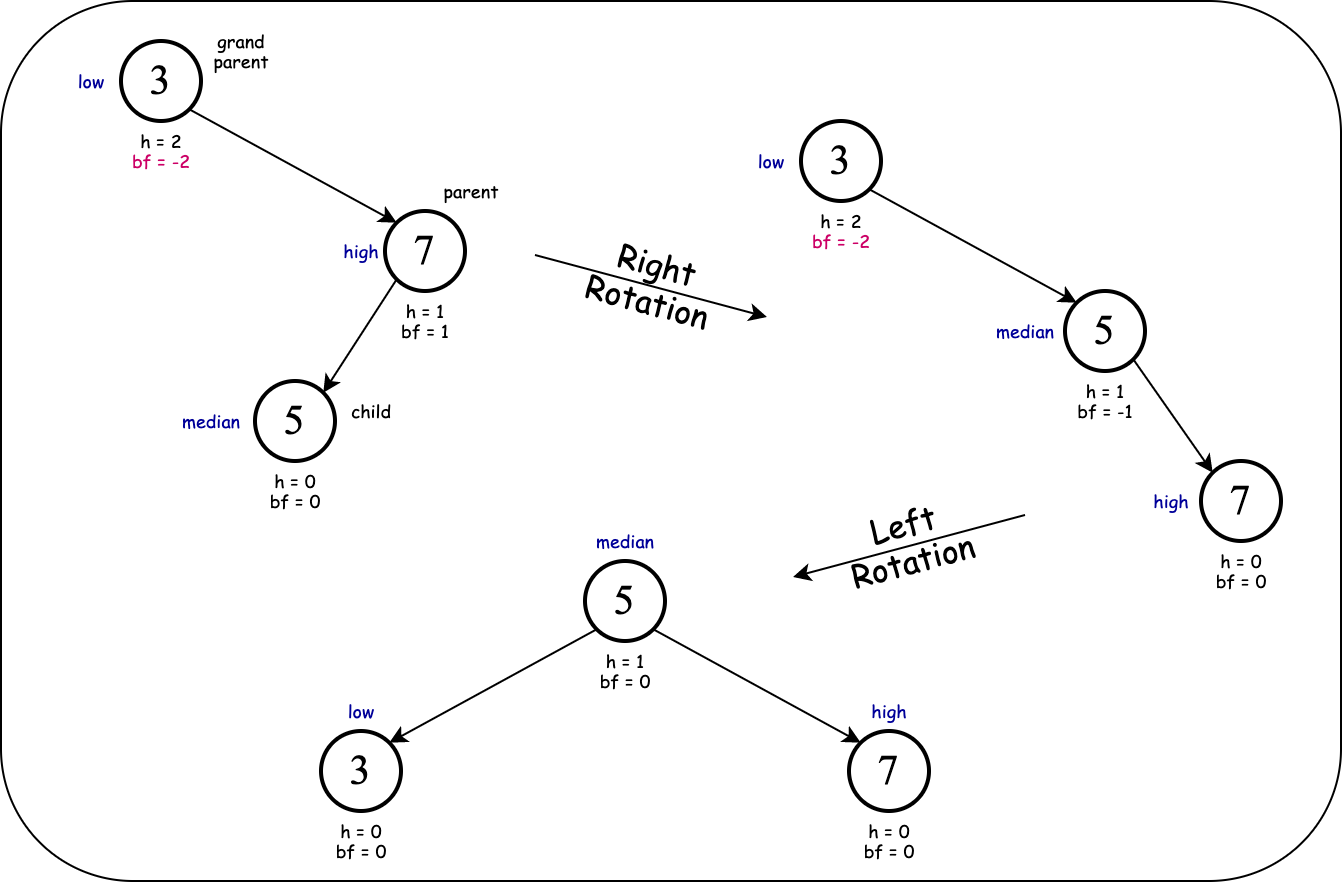
Notice the violation of balance property occurred in the grand parent of the newly inserted node. From the perspective of the grand parent node, the problem was caused in right child's left subtree. The solution is a (double) right-left rotation to bring the median value above the high and low values.