Spanning Tree

A spanning tree of a connected undirected graph $G$ is a subgraph of it (every edge in the tree belongs to $G$) that spans $G$ (it includes every vertex of $G$).

Consider this graph:

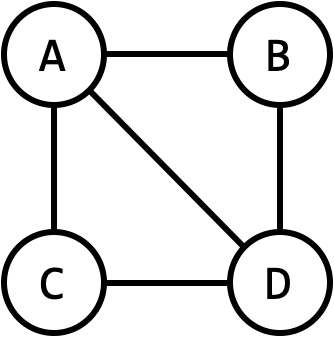
Every tree below is a spanning tree of the graph above.

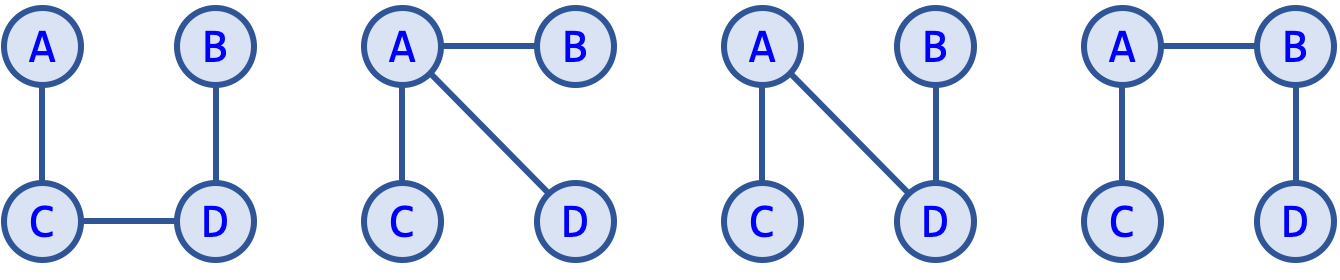
As it can be seen above, a graph may have several spanning trees.

A spanning tree can be built by doing a BFS/DFS of the graph.

Recall the demo for BFS/DFS from prior chapters:

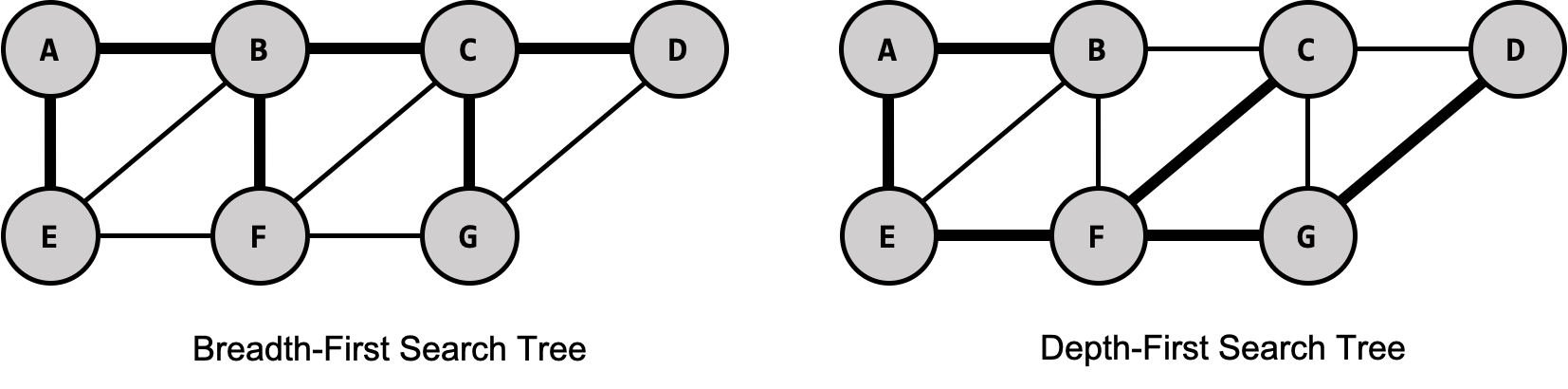
The spanning trees consist (only) of the thick edges.

Resources