Putting it all together!

This is called a (single) right rotation:

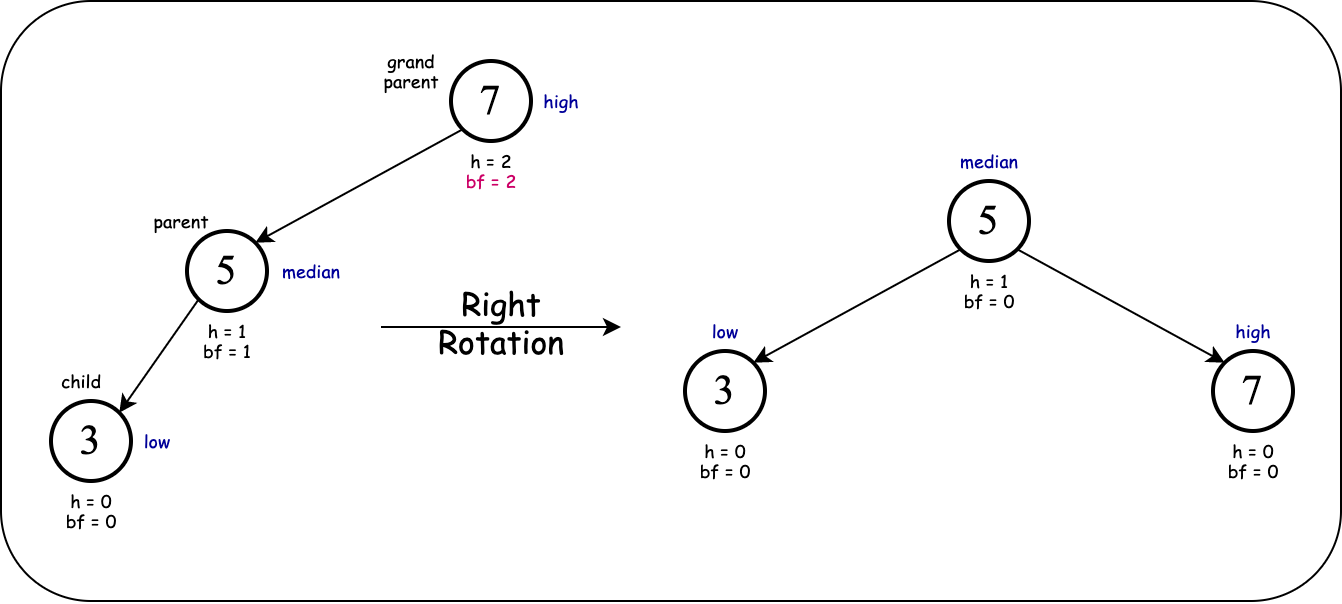
Cause of imbalance: left child's left subtree.

This is called a (single) left rotation:

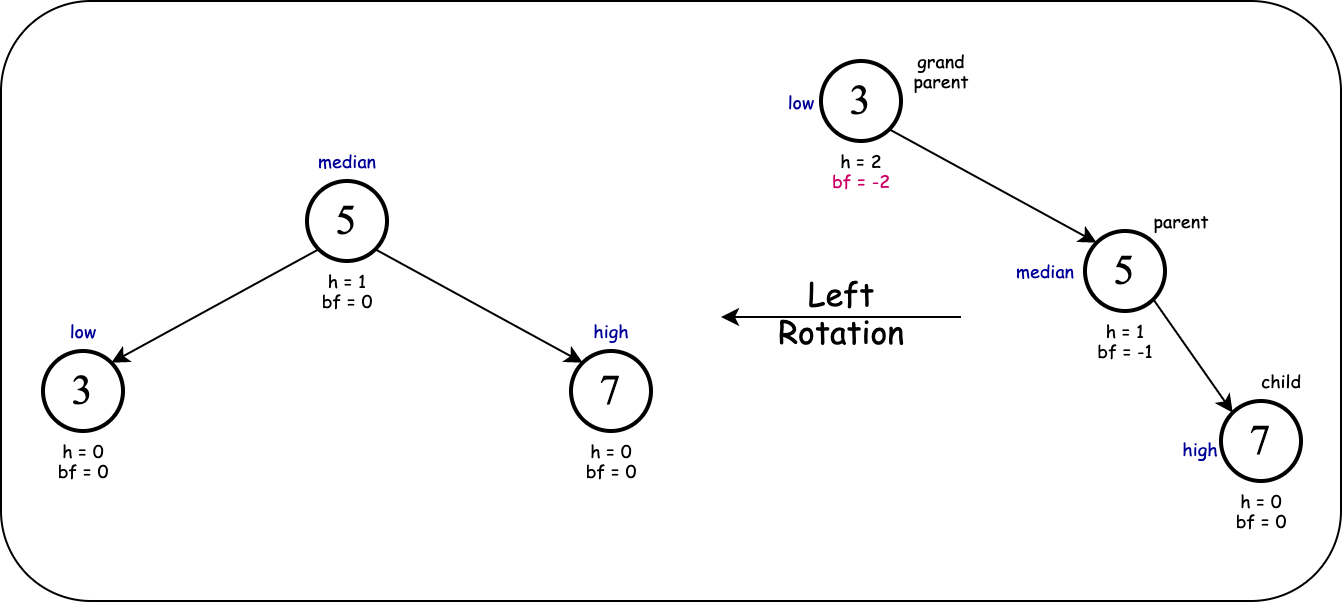
Cause of imbalance: right child's right subtree.

This is called a (double) right-left rotation:

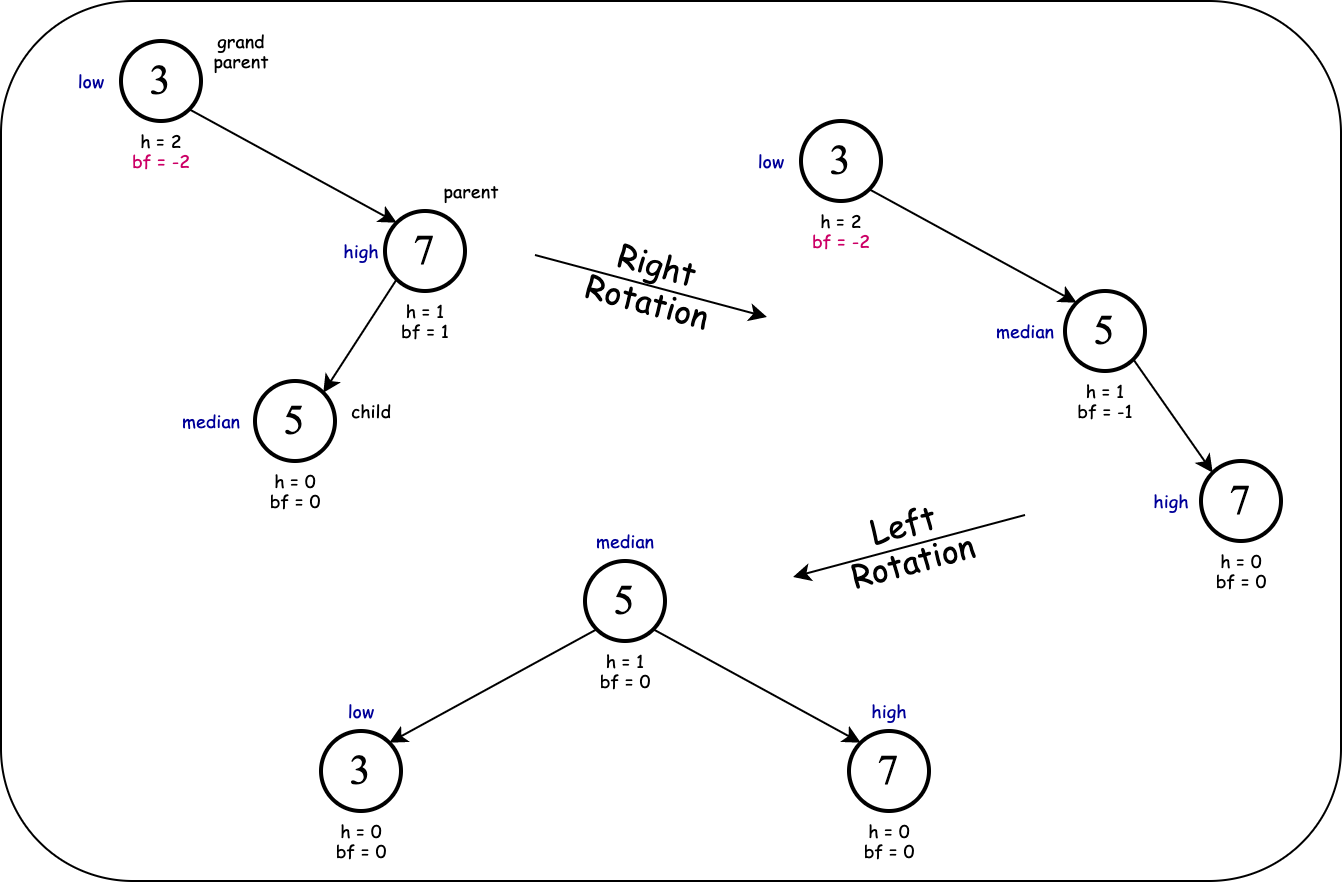
Cause of imbalance: right child's left subtree.

This is called a (double) left-right rotation:

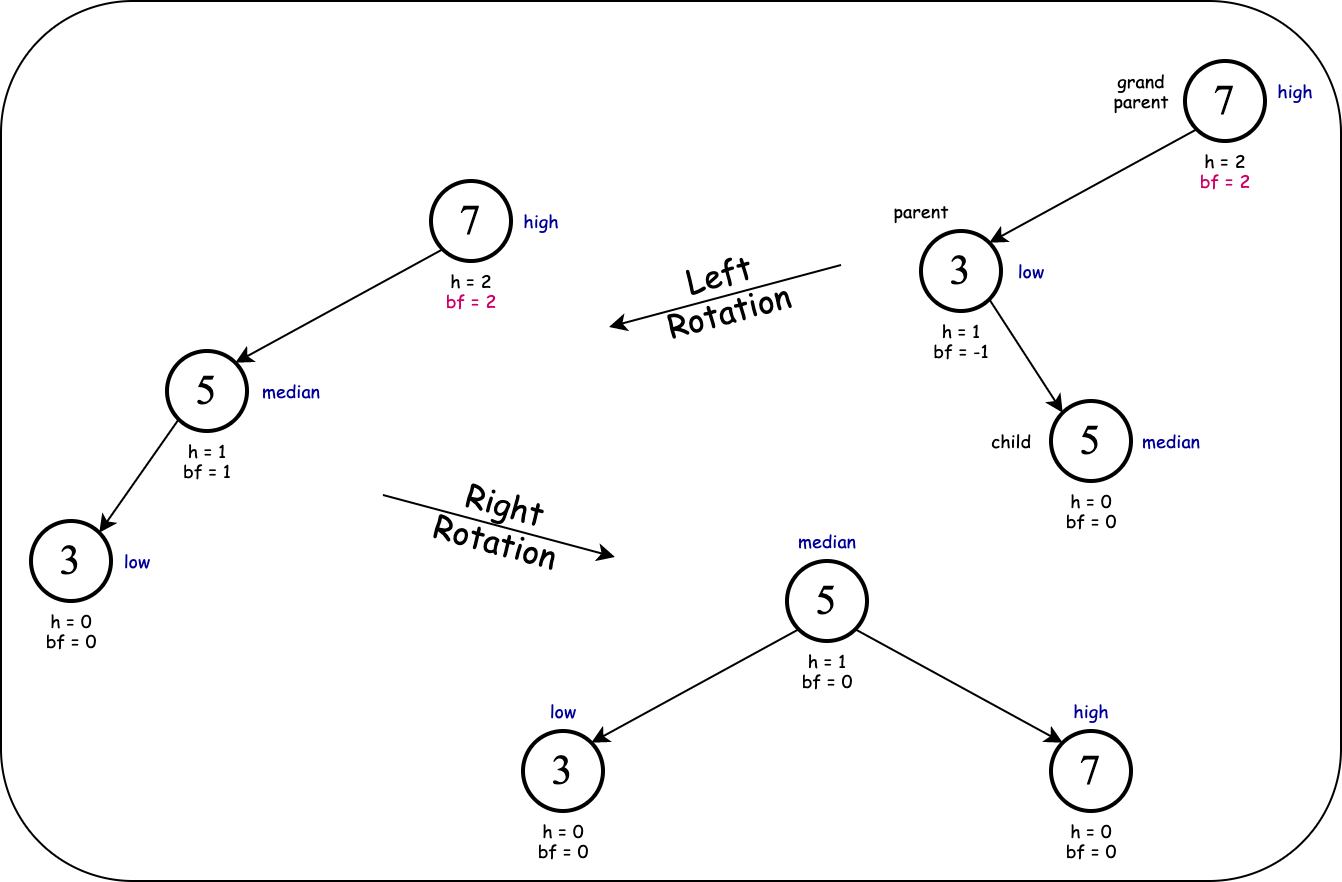
Cause of imbalance: left child's right subtree.

Exercise Complete the following table which assists in determining type of rotation.

Imbalance NodeChild's bf = -1
(right heavy)		Child's bf = 1
(left heavy)
bf = -2
(right heavy)
bf = 2
(left heavy)
Solution
Imbalance NodeChild's bf = -1
(right heavy)		Child's bf = 1
(left heavy)
bf = -2
(right heavy)		LeftRight-Left
bf = 2
(left heavy)		Left-RightRight

Caution The table above does not account for an edge case where the child's balance factor is $0$.

Schematic representation of tree rotations
Resources