Tree Terminology: Height
The height of a node $n$ is the length of a longest path from $n$ to a leaf.
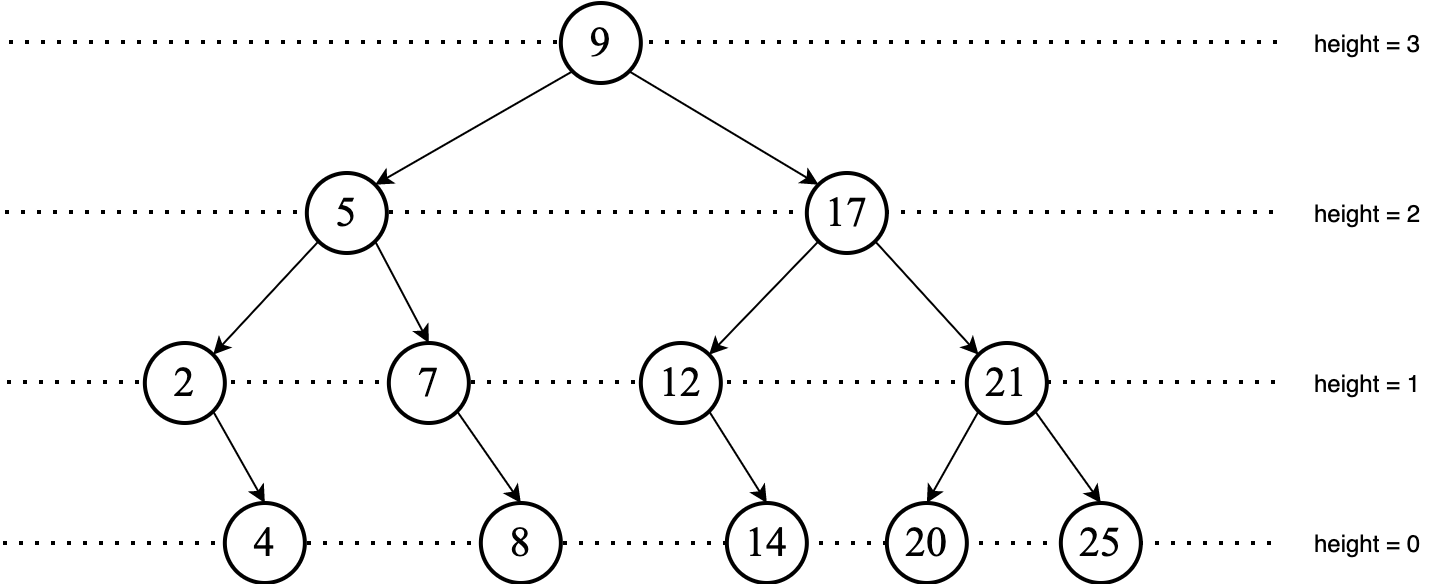
The height of the tree is the height of the root.
We can recursively define height of a node as follows:
$$ \text{height}(n)=\left \{ \begin{matrix} 0 & n = \text{leaf} \\ 1 + \max(\text{height of children}) & n \neq \text{leaf} \end{matrix} \right \} $$
Aside: In some references, the height of a node includes the node. In that case, the height of a leaf node is 1.