Post-order Traversal: Left, Right, Root!

This is the strategy for post-order traversal:

For every node, visit its left subtree, then visit its right subtree, then visit the node.

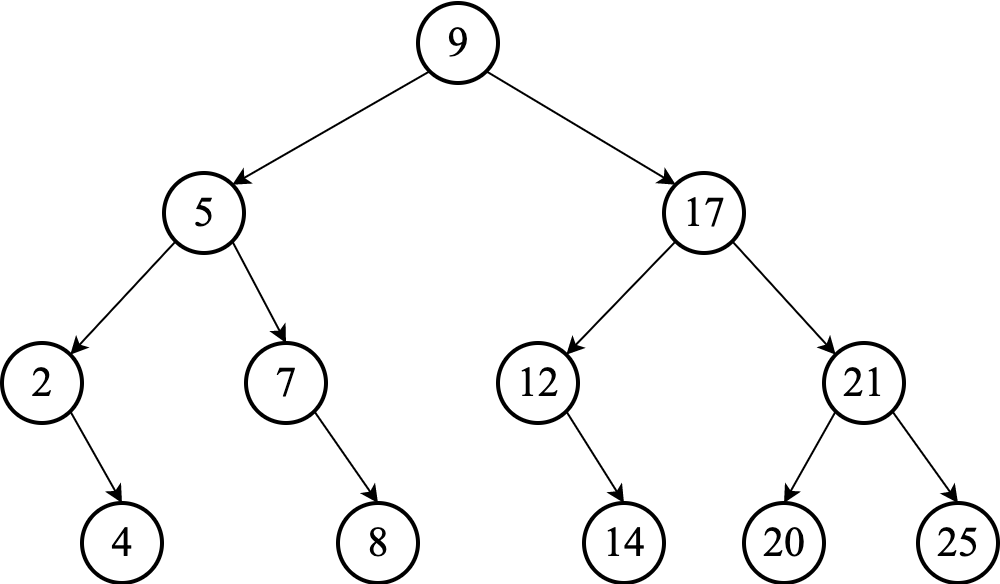
Following the strategy above will generate this sequence:

$$ 4, 2, 8, 7, 5, 14, 12, 20, 25, 21, 17, 9 $$

Explanation

We start with the root, $9$, but we must first visit its left subtree. So we move to $5$, but we must first visit its left subtree. So we move to $2$. We must visit the left subtree of $2$ but there is none. So we move to visit the right subtree of $2$ which is rooted at $4$. We must however first visit the left subtree of $4$. Since there is no left subtree to $4$, we move to visit its right subtree. There is, however, no subtree to the right of $4$. So we can visit $4$ itself. Now we are done with the right subtree of $2$, so we can visit $2$ itself.

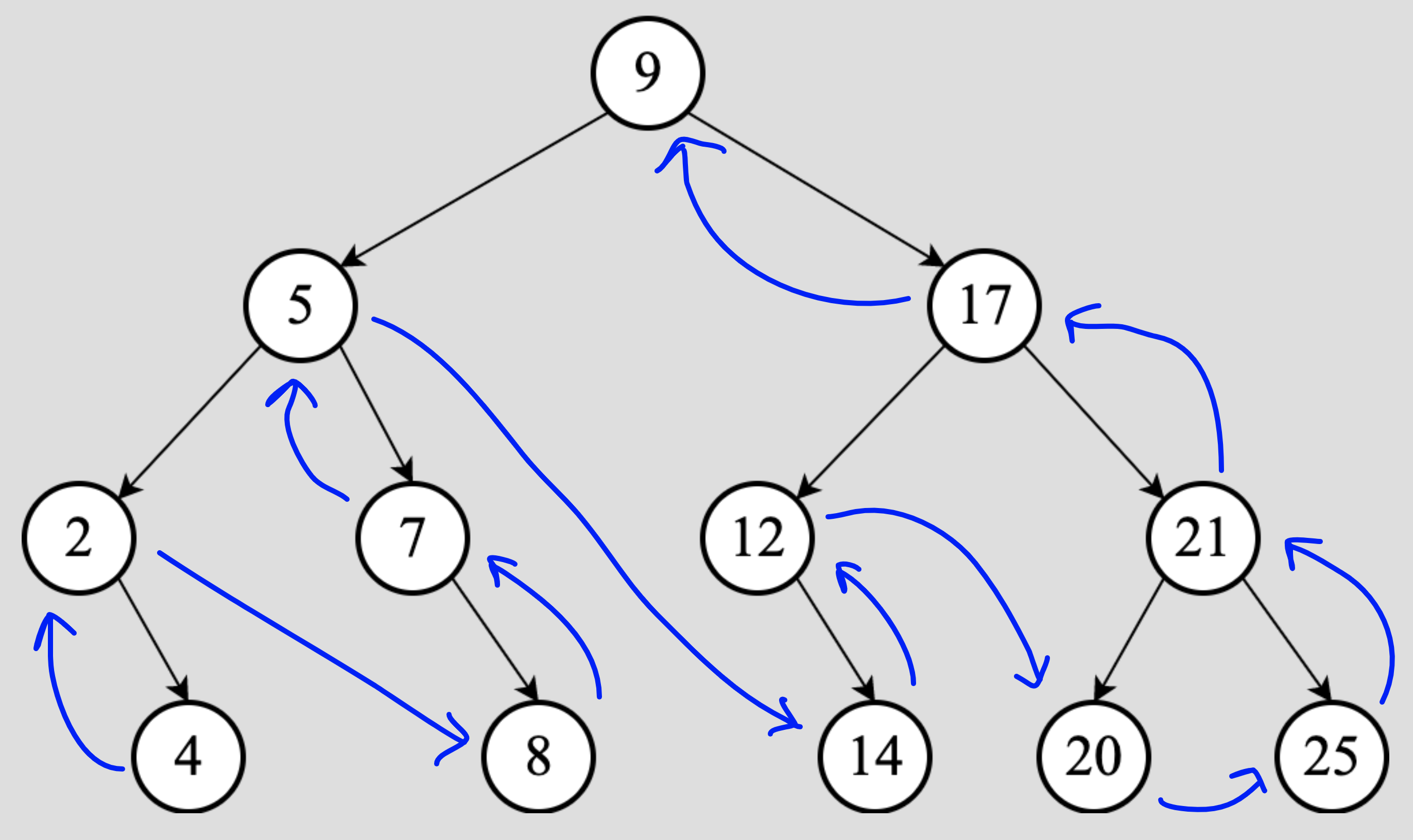
Now we are done with the left subtree of $5$. We must visit the right subtree of $5$ now. So we move to $7$, but we must first visit its left subtree. There is no subtree to the left of $7$ though. So we can move to the right subtree of $7$. Therefore, we move to $8$. We must now visit the left subtree of $8$ but there is none. So we move to visit the right subtree of $8$ but there is none. We can therefore, visit $8$ itself. Once $8$ is visited, we are done with the right subtree of $7$, so we can visit $7$ itself. Once we have visited $7$, we are done with the right subtree of $5$, so we can visit $5$ itself. Once we have visited $5$ we are done with the left subtree of $9$, so we must move to visit the right subtree of $9$ $\dots$

Here is a recursive definition of post-order traversal: for each node, recursively perform post-order traversal of its children (the subtrees rooted at its left and right child, in that order), then visit the node itself.

Resources