Tree Terminology: Depth
The depth, or level, of a node $n$ is the length of the path from the root to $n$.
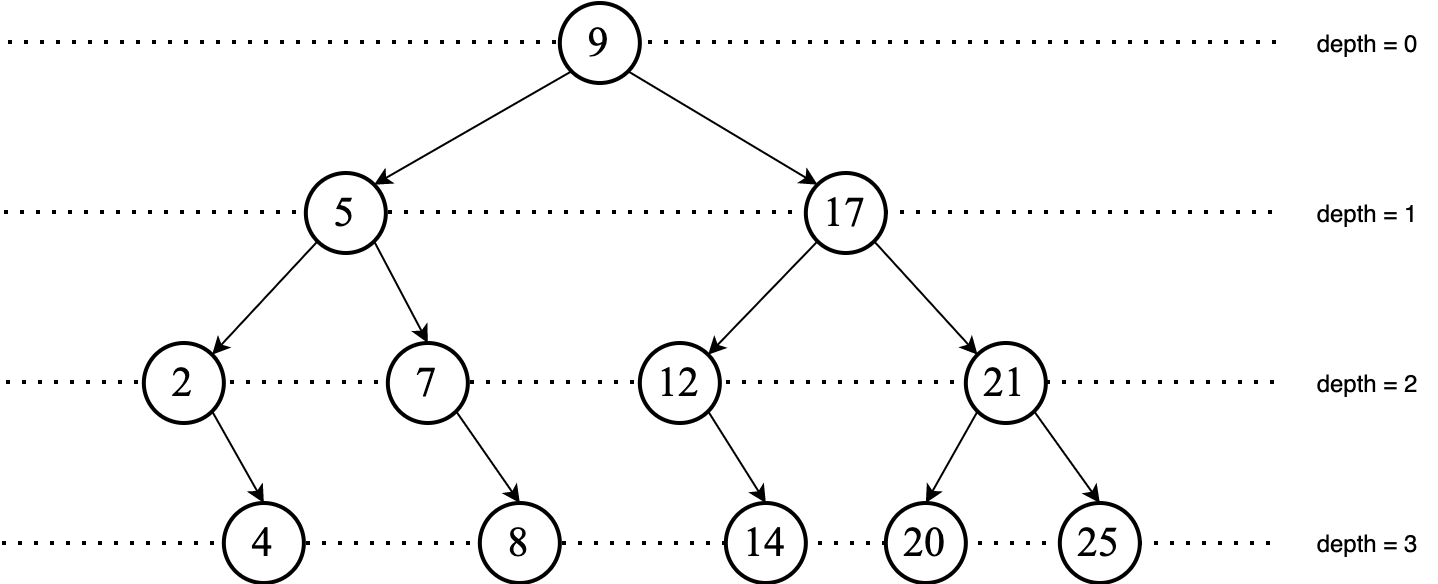
The height of the tree is the depth of the deepest node.
We can recursively define depth of a node as follows:
$$ \text{depth}(n)=\left \{ \begin{matrix} 0 & n = \text{root} \\ 1 + \text{depth}(\text{parent}(n)) & n \neq \text{root} \end{matrix} \right \} $$
Aside: In some references, the depth of a node includes the node. In that case, the depth of the root is $1$. Some references keep the depth of the root at $0$ but define $\text{level} = \text{depth} + 1$ so the level of the root is $1$.