Minimum Spanning Tree

Many applications of spanning trees include finding not any spanning tree, but one whose total edge weight is minimal among all the possible spanning trees, a so-called minimum weight spanning tree (MST).

A minimum spanning tree of a weighted graph $G$ is a spanning tree of it with the minimum possible total edge weight.

Consider the following weighted graph:

Every tree below is a minimum spanning tree of the graph above.

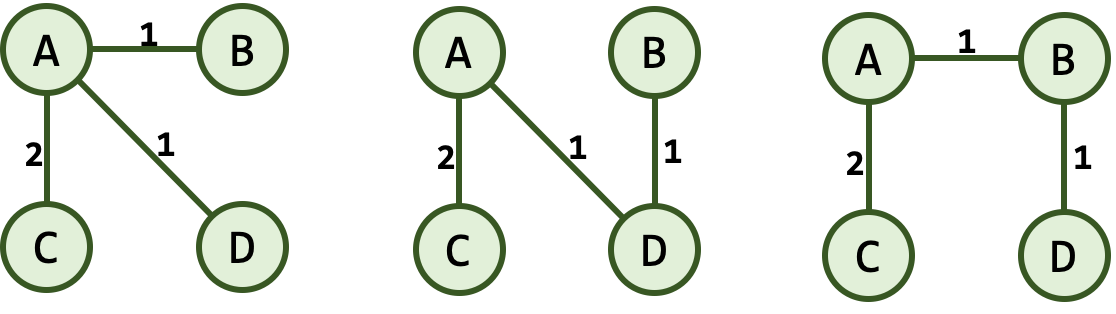
As it can be seen, an MST is not necessarily unique. There may be several minimum spanning trees of the same total weight. If each edge has a distinct weight then there will be only one, unique minimum spanning tree.

Minimum Spanning Tree Problem

Given a connected, undirected weighted graph $G = (V, E, w)$, the minimum (weight) spanning tree problem requires finding a spanning tree of minimum weight, where the weight of a tree $T$ is defined as sum of the wight of all its edges:

$$ w(T) = \sum_{e \in E(T)} w(e) $$

We will look at two algorithms to solve the MST problem:

  • Prim's Algorithm
  • Kruskal's Algorithm
Resources