Insertion Sort: The Algorithm

You are asked, as part of homework-3, to implement the Insertion Sort algorithm. This lesson helps you to understand the insertion sort process.

In Insertion Sort, we divide the list into two parts, a sorted and an unsorted part. At each iteration, insertion sort removes one element from the unsorted part, finds the location it belongs within the sorted part, and inserts it there. It repeats this process until no elements remain in the unsorted part.

Demo

The following slides assist in building an intuition for the insertion sort:

Here is the process described in pseudocode. 

for i gets values from 1 to length-1
  j gets i
  while j > 0 and val[j] < val[j-1]
    swap val[j] and val[j-1]
    decrement j by 1
  // at this point, all elements to the left of index i are sorted.

Imagine running the insertion sort algorithm on the following sequence of values:

$$ 14, 10, 23, 34, 6, 17, 50, 14 $$

Exercise Complete the following trace table.

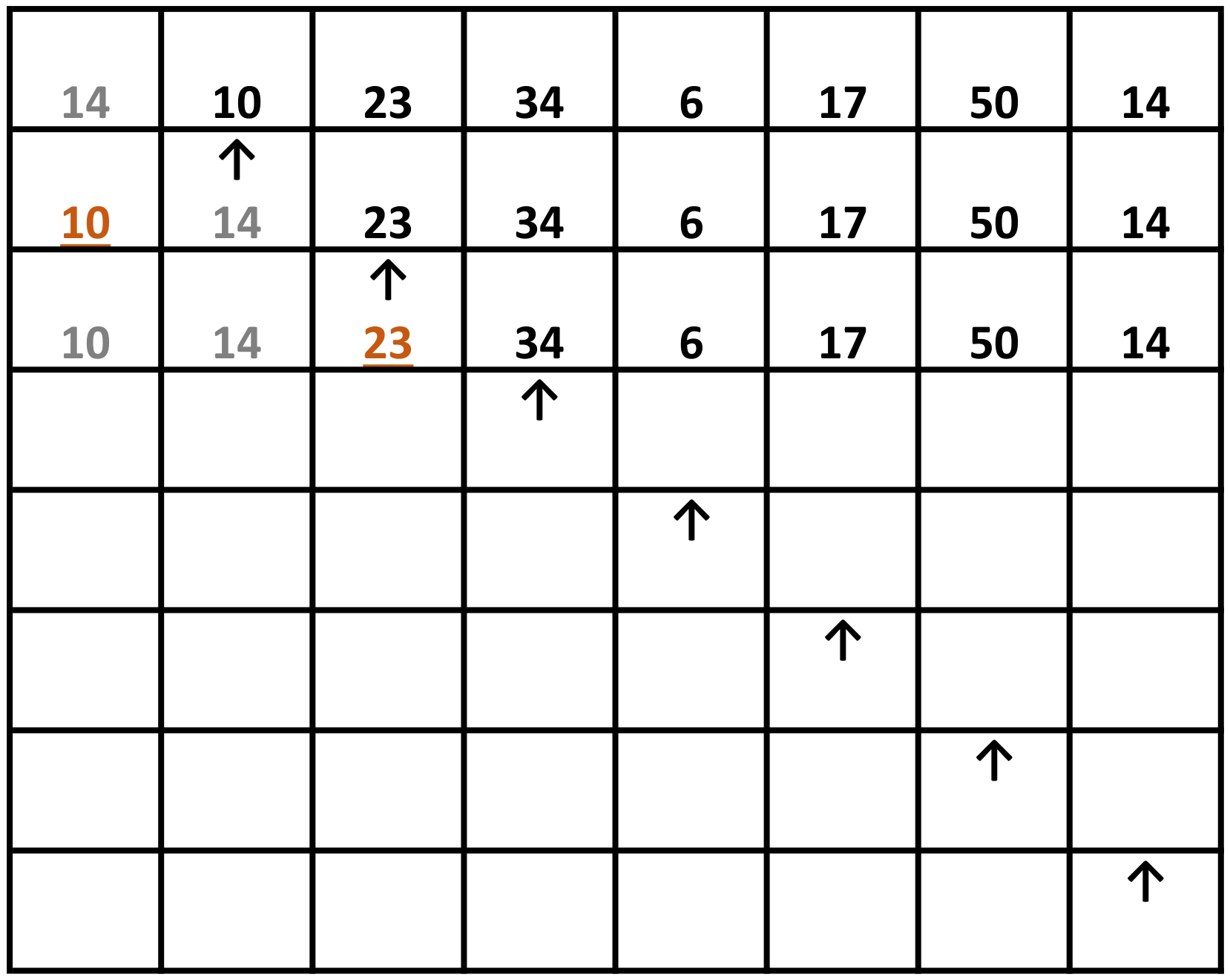
Making sense of the table!

Each row of the table above represents a complete inner pass through the insertion sort algorithm. Two complete passes have been filled as an example of the sort. You are responsible for attempting to manually perform the insertion sort algorithm on the remaining passes through the data. The upwards arrow in each row indicates which element needs to be partially sorted next (in other words, sorted with respect to all elements to its left).

Solution

Exercise Analyze the running time of the insertion sort algorithm. In particular, think about where comparisons and swaps are being made, and how many of them occur in each pass through the collection to be sorted.

Solution

The algorithm has a quadratic running time, i.e. $O(n^2)$.

Looking at the pseudocode:

  • Each inner pass has a comparison and swap for as many positions as it needs to move the next element into its sorted spot, which at max is the number of elements in the partially sorted part of the array.

  • In the worst case, when one has an array in descending order, each next element would need to be moved all the way to the beginning of the array.

  • There would then be $1 + 2 + \dots + (n-1) = \frac{n(n-1)}{2}$ comparisons and swaps, where $n$ is the number of elements; the time complexity of the worst case is $O(n^2)$.

Insertion sort requires $O(n)$ space: $O(n)$ input and $O(1)$ auxiliary space.

Resources