Task 3

Assume the following directed graph represents the bus stops in a small neighborhood. Each vertex is a bus stop. The edges are one-way streets.

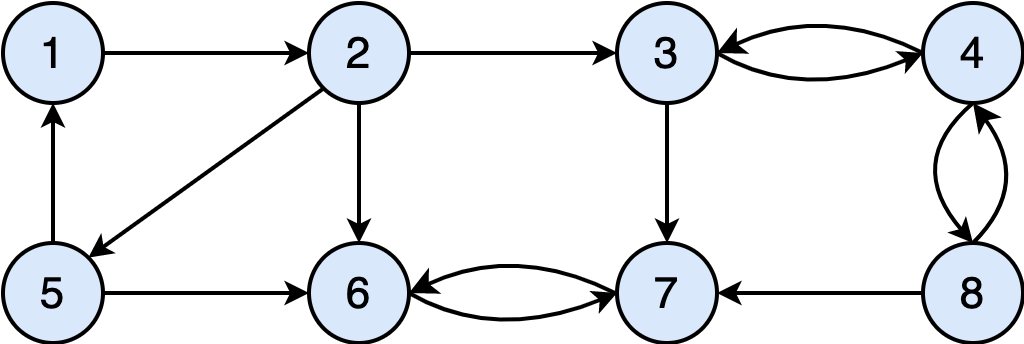
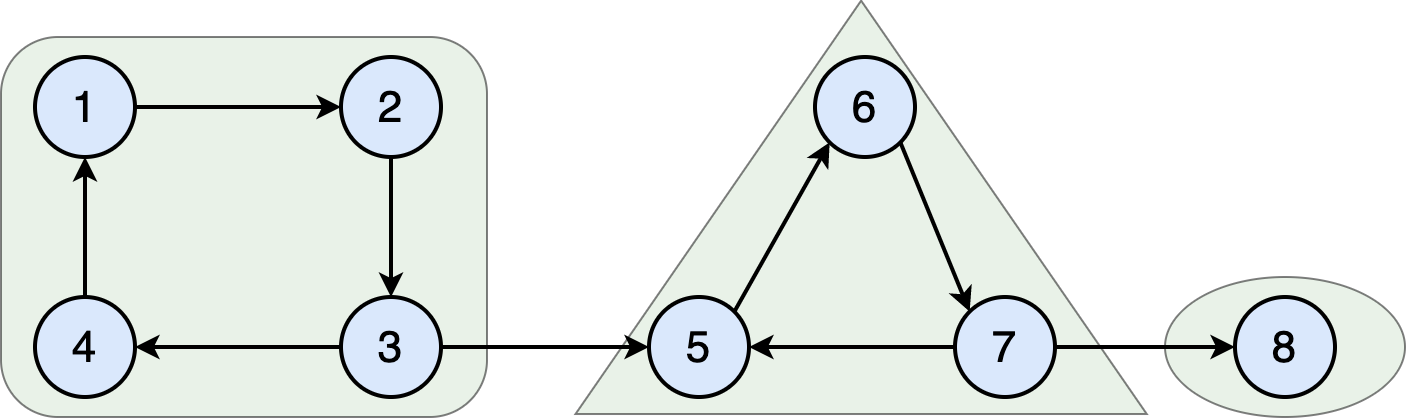
Notice we can cluster the bus stops as follows:

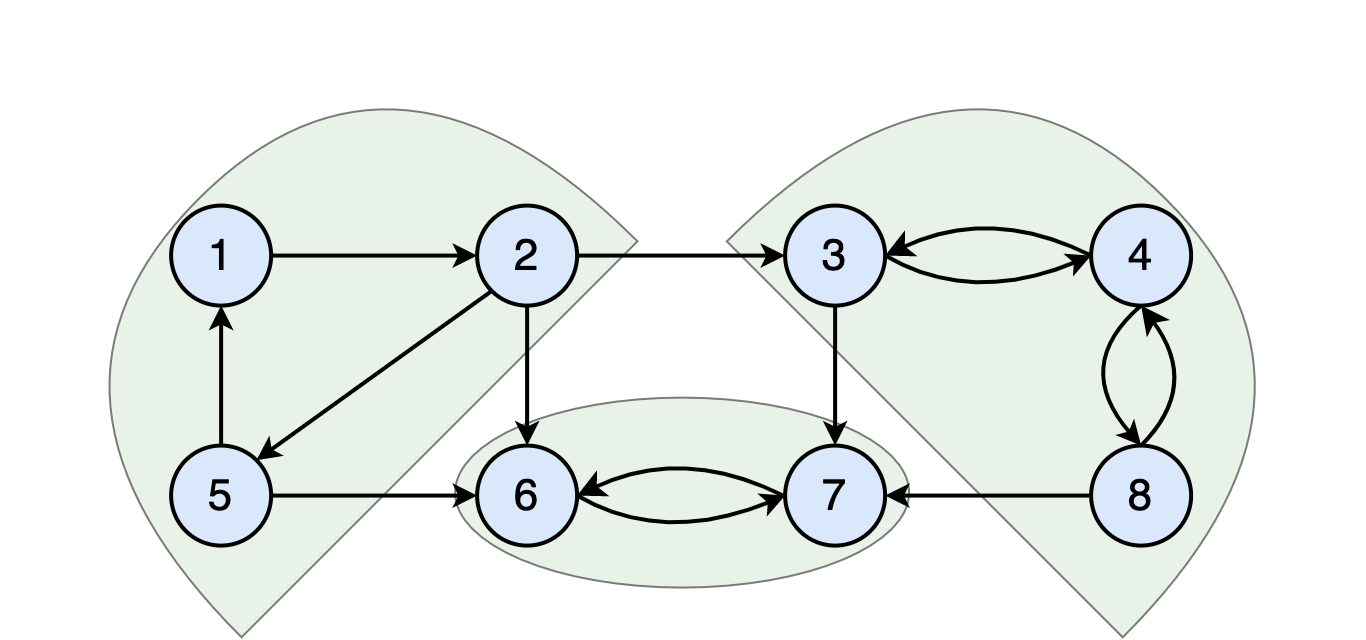
In each cluster, all vertices are reachable from any other vertex in that cluster.

For example, in the cluster that contains vertices ${1, 2, 5}$, you can start at any of these vertices and visit the other two. You can do the same for the vertices in the cluster ${3,4,8}$ and ${6,7}$. On the other hand, although it is possible to, e.g., start at $2$ and visit $7$, there is no path from $7$ to $2$. Thus, $2$ and $7$ are not in the same cluster.

In this task, we are interested in writing a program that, given a graph in a standard format, outputs the number of clusters that exhibit the aforementioned property.

First, let's ensure we can cluster a given graph on paper.

Example 1

Draw the graph corresponding to the following input and count the number of clusters it has.

Input:

4 4 
1 2 
4 1 
2 3 
3 1

Output

?

Solution

The graph has 2 clusters.

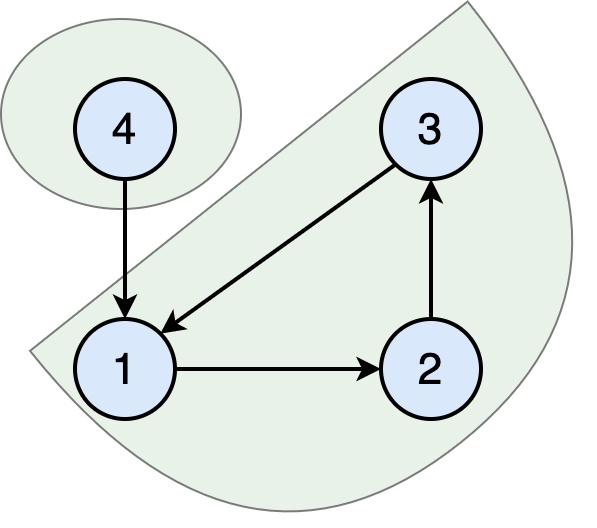
Notice how one cluster is made entirely up of the single vertex ${4}$; you may interpret this as vertex 4 is reachable from itself.

Example 2

Draw the graph corresponding to the following input and count the number of clusters it has.

Input:

5 7 
2 1 
3 2 
3 1 
4 3 
4 1 
5 2 
5 3

Output

?

Solution

The graph has 5 clusters

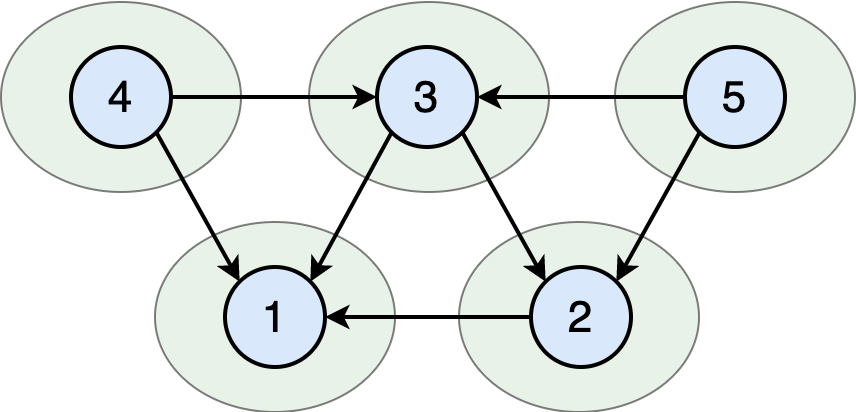
Example 3

Draw the graph corresponding to the following input and count the number of clusters it has.

Input:

8 9 
1 2 
2 3 
3 4 
4 1 
3 5 
5 6 
6 7 
7 5 
7 8

Output

?

Solution

The graph has 3 clusters

Slow Solution

For any given vertex $v$, we can run a graph search algorithm such as DFS to find all the vertices $u$ that are reachable from $v$. Then, for each reachable vertex $u$ we can rerun DFS and see if $v$ is reachable from $u$ too. For any such $v$ and $u$ where there is a directed path from $v$ to $u$ and from $u$ to $v$, the vertices $u$ and $v$ are in the same cluster. This approach is obviously slow since you must run DFS $O(N)$ times where the runtime of DFS itself is $O(N+M)$ , resulting in $O(N^2+NM)$ runtime.

Linear-time Solution

We can find all clusters in linear time by running DFS twice! The idea is to run DFS once on the graph to find all connected components. Then reverse the direction of all the edges and rerun DFS. If $u$ is reachable from $v$ in both the (original) graph and when the edges are reversed, then $u$ and $v$ are on the same cluster.

The following demo presents this algorithm in more details.

You must complete the implementation of Task3.numberOfClusters according to the demo. Your implementation must closely follow the demo. Here are a few tips:

1. Computing the reverse post-order traversal is an integral part of the solution. Let's elaborate a bit on that. Suppose you have the following directed graph.

   

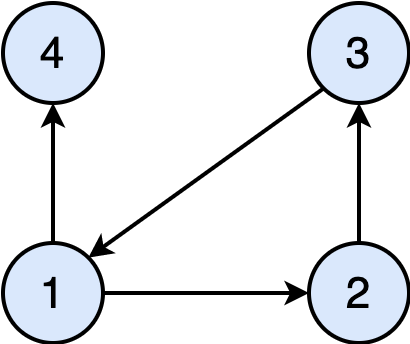
   If we perform DFS starting at vertex-1, assuming the DFS visits neighbors in numerical order, it would visit the vertices 1, 2, 3, 4 in that order. This is pre-order traversal: visit a node and then its neighbors. To perform post-order, we must delay marking a node as explored, after its neighbors have been explored. In that case, the post-order DFS will be 3, 2, 4, 1. The reverse post-order would be 1, 4, 2, 3. The use of Stack and recursive DFS allows you to easily capture the reverse post-order traversal.

2. Consider the following graph, which is similar to the one above, except that the edge (1,4) is reversed.

   

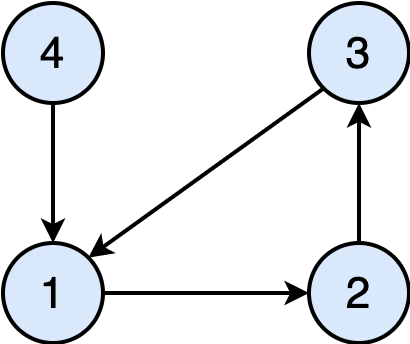
   If you perform DFS starting at vertex-1, you will never reach vertex-4. This is okay if the goal is to find all the reachable vertices from vertex-1. However, when the goal is to find all connected components, we must perform DFS on the entire graph. Therefore, you must rerun DFS for vertices that are not explored.

   for every vertex s in graph:
       if s is not explored:
   	    run dfs starting at s
   

A few test cases are provided in Task3Test.java file. You are encouraged but not required to add more tests.