PriorityQueue Aside: Linked Tree Representation
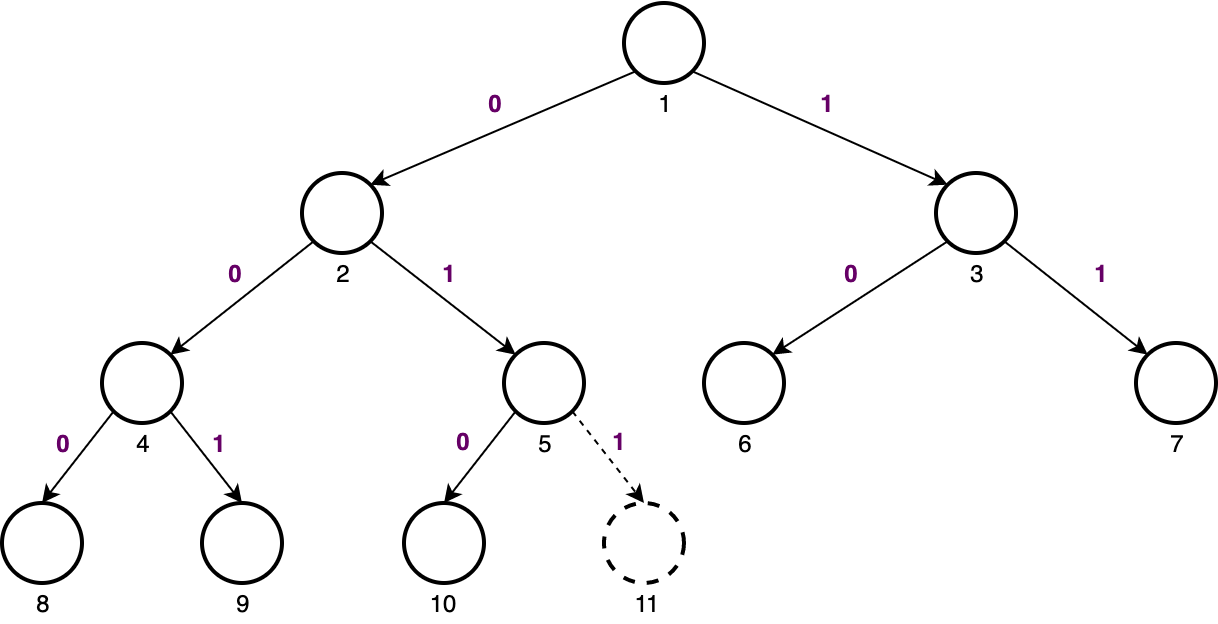
Exercise Suppose that a binary heap with $n$ nodes are stored in linked structure (not an array). How can you get (find) the node (position) where the next leaf should be added in $O(\lg n)$ time?
Solution
We can employ a clever trick based on binary numbers in conjunction with the ranked representation. Suppose we have already $10$ nodes in the binary heap and we want to insert the $11^{\text{th}}$ node. We know the binary representation of $11$ is $1011$:
$$ 11_{10} = 1011_{2} $$
Now take the first digit (from left) of the binary representation to mean "start at root" and for each remaining digit (from left to right) in the binary representation of the $k^{\text{th}}$ node, go left if the digit is $0$ and go right if it is $1$: