Task 3
Max is working for the university library. The library has a few buildings scattered around the campus. For the convenience of the students, the library allows returning borrowed books to any of the buildings. The reception collects the books and piles them up on a cart for Max to transfer between the buildings.

As you can see in the image above, each "book cart" contains two "book piles". The reception usually does a sloppy job of piling the books:

When Max moves the book cart around, the books fall off the cart if larger/heaver ones are placed on top of smaller ones. Max, therefore, "sorts" the books in each pile before transporting the cart.

One strategy is to take off all books in a pile and put them back on in order: larger books first. This is "selection sort" which has $O(n^2)$ runtime. Max believes to have found an strategy that does this in $O(n)$. I explain Max's strategy by simplifying the problem and using numbers instead of books.
Here are the initial and goal states:
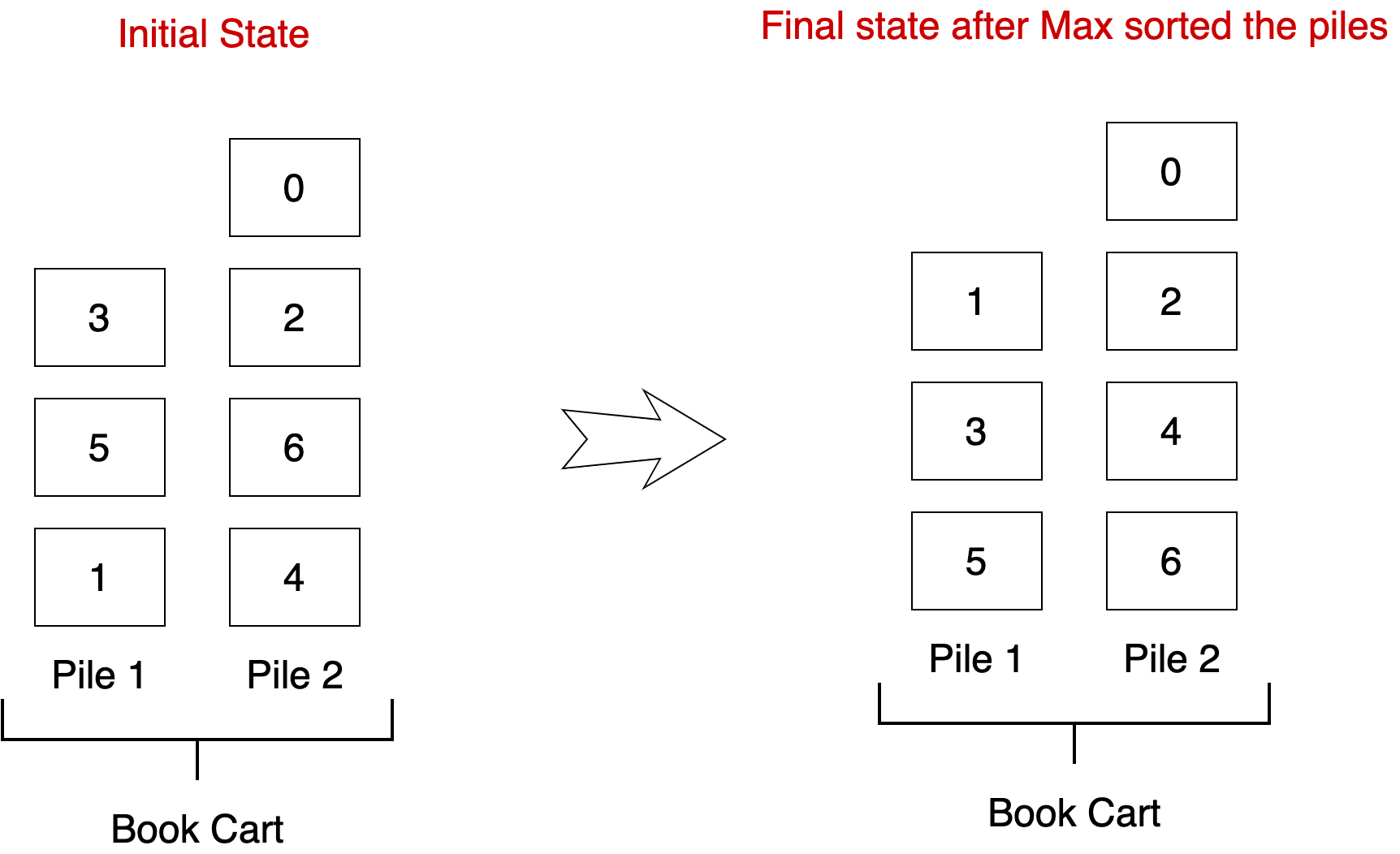
And here are the steps that Max performs to sort pile-1:
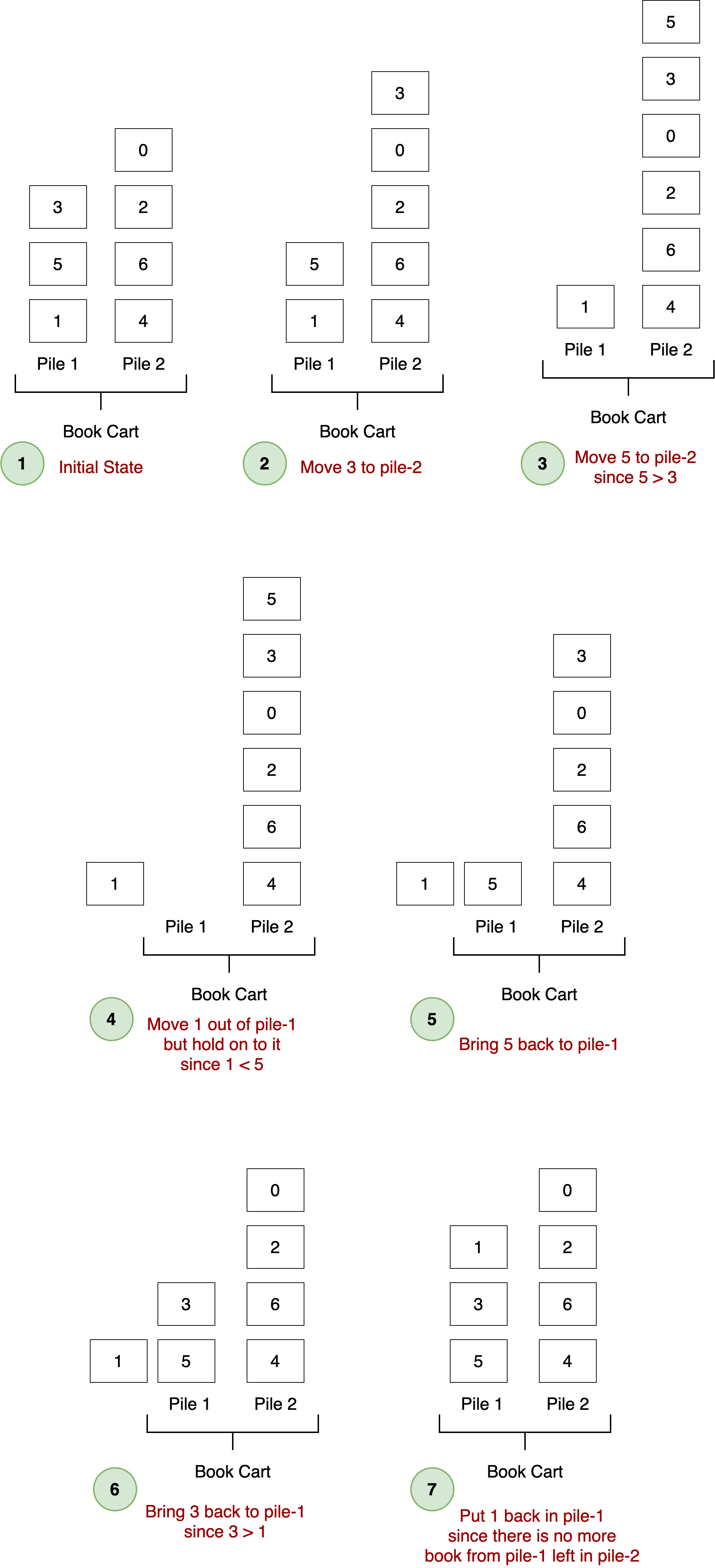
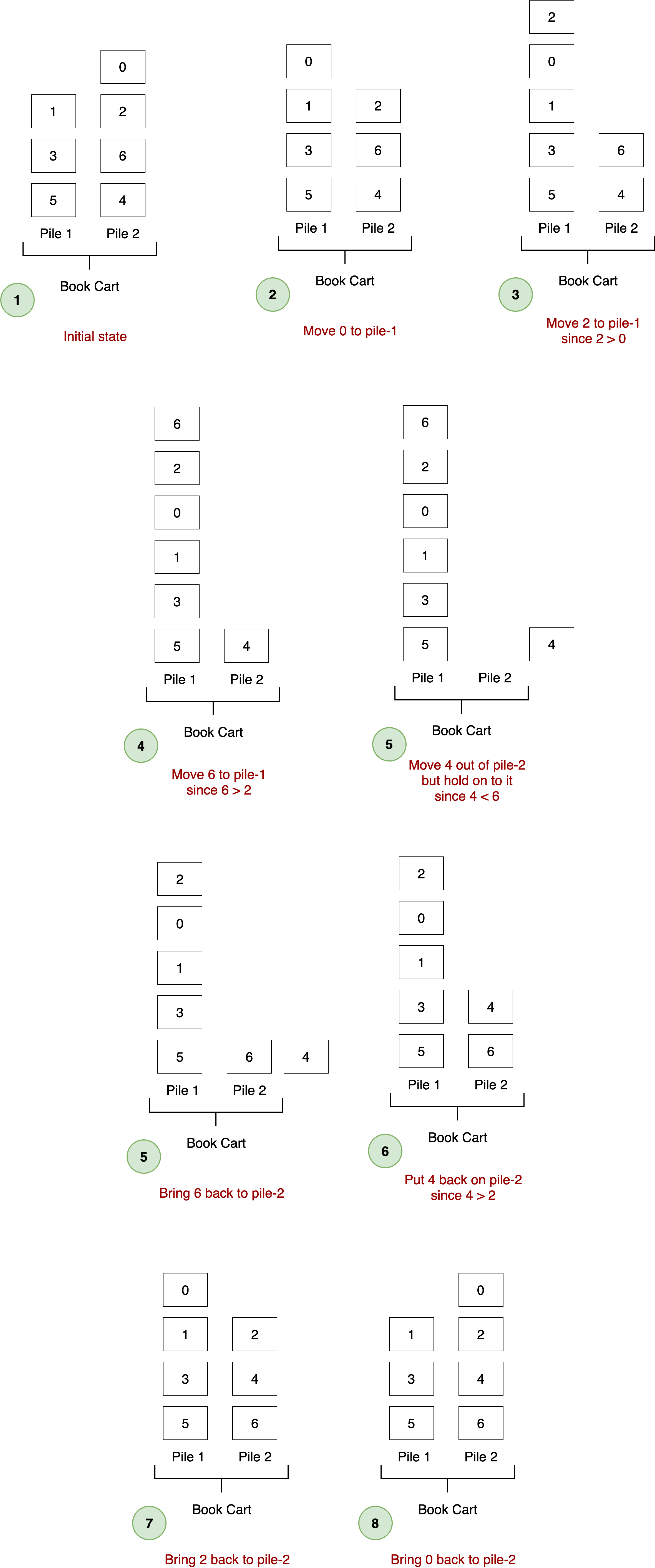
Before moving any further, try to apply Max's strategy to sort pile-2.
Solution
Notice inside task-3 package, you are given the following classes:
Book— represents a book; since the book size/weight matters to Max, we crudely represent a book simply with its number of pages.BookPile— represents a pile of books; essentially a wrapper class around Java'sStack.BookCart— represents the book cart that Max uses to transfer books between buildings. Thepilesarray is used to represent the two piles of books in each book cart.
You have three sub-tasks to complete:
- Add at least three test cases for
BookCart.sorttoBookCartTest. Test cases must be sufficiently different (i.e., testing different scenarios; for instance a case where one of the piles is empty or one of the piles is already sorted, etc.)- Implement
BookCart.sortaccording to Max's sorting strategy.- In the
README.mdfile, under "Max's Sorting Strategy," (briefly) argue if Max's strategy is really $O(n)$ or not? (If not, what is the time complexity of it?)
Note: the iterator of BookCart goes over the two sorted (book) piles in a way the resulting iteration produces a single sorted sequence. It works only if the two piles are sorted (i.e. if your implementation of sort is correctly working). So, you can use the iterator in your tests for checking if the sort was implemented correctly. An example is given in BookCartTest.