Shortest Path: Weighted Graph
Recall: A weighted graph is a special type of a labeled graph in which the edge labels are numbers.
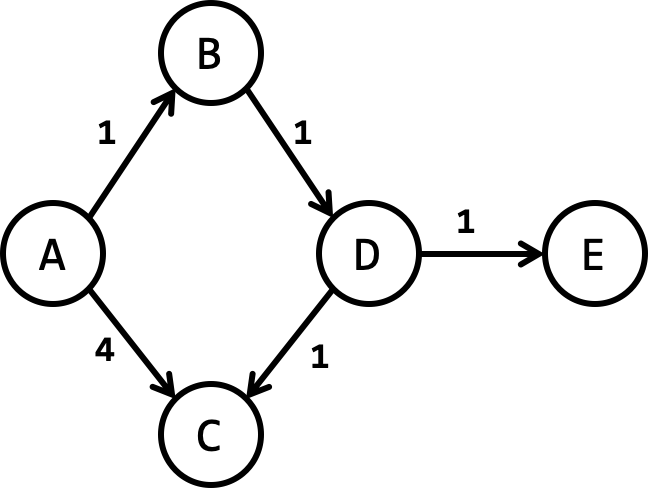
Notice in the graph above, there are two paths between $A$ and $C$, the shortest in terms of length is $(A, C)$. However, the shortest (cheapest) in terms of total weight (cost) is $(A, B, D, C)$.
The shortest path problem is generally defined in terms of "cost". We can set the edge weights to $1$ and that would give us the shortest path in terms of length.
Exercise Can BFS be used to find the shortest path when shortest means "cheapest"?
Solution
BFS will not work as it can be seen in the example graph. BFS will explore $B$ and $C$ at the same time (both are one edge away from $A$) and concludes the shortest path from $A$ to $C$ is the direct edge $(A,C)$. BST will not update this "shortest" path when it finds the second path (which actually is cheaper) from $D$ to $C$ because at that point $C$ is already "explored".