Asymptotic Order of Growth

Here are the common running times in order of increasing growth rate.

  • $O(1)$ — Constant functions
    • Running time does not depend on the input size.
    • It does not mean it only takes one step!
  • $O(\log n)$ — Logarithmic functions
    • Also called sub-linear functions.
    • Runtime grows slower than the size of the problem.
    • Example: Binary Search.
  • $O(n)$ — Linear functions
    • Running time is proportional to input size.
    • Example: Linear search.
  • $O(n\log n)$ — Superlinear functions
  • $O(n^2)$ — Quadratic functions
    • Running time is proportional to the square of the input size.
    • Example: Bubble/Insertion/Selection sort (we'll cover later).
  • $O(n^k)$ — Polynomial functions
    • $k$ is a constant $>1$
    • $O(n^2)$ is a special case of this
    • Example: Enumerate all subsets of $k$ nodes among $n$ nodes.
  • $O(c^n)$ — Exponential functions
    • $c$ is a constant $>1$
    • Example: Enumerating all subsets of $n$ items.
  • $O(n!)$ — Factorial functions
    • Example: Generating all permutations or orderings of $n$ items.

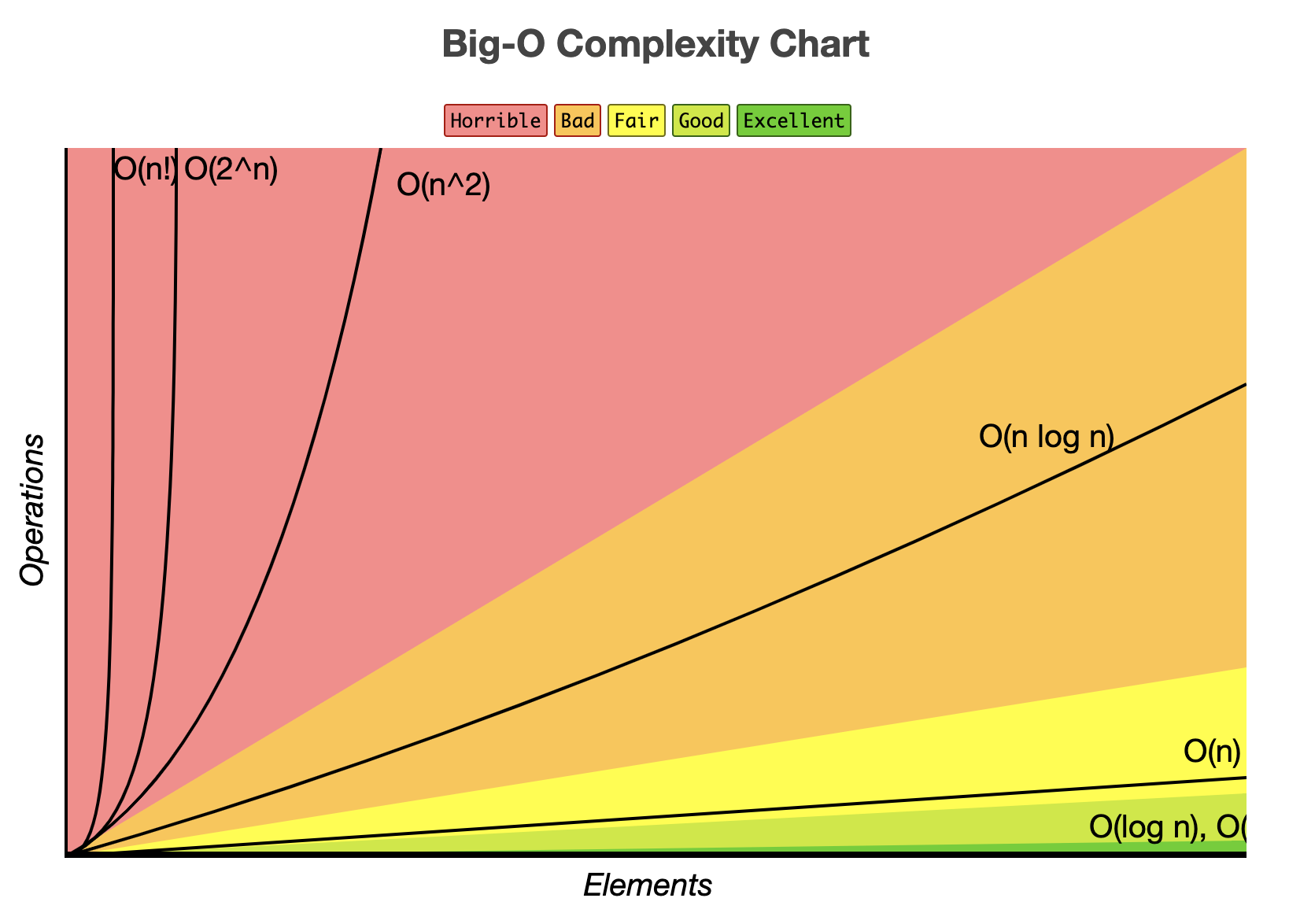
All you really need to understand is the order of increasing growth rate:

$$ n! \gg 2^n \gg n^3 \gg n^2 \gg n\log n \gg n \gg \log n \gg 1 $$

There are other (more esoteric) functions that arise in the study of algorithms. However, the functions above account for describing the runtime of most algorithms in practice.

The following illustration is taken from bigocheatsheet.com:

Resources

This article contains explanation of big Oh notation, common running times, and a good looking plot of common runtimes.