The Gist!

It turns out, in an expression like $12754n^{2} + 4353n + 834\lg n + 13546$, those constant factors will change based on how you express an algorithm.

For example, consider these two code snippets:

public void countUp(int num) {
  for (int i = 1; i <= num; i++) {    
      System.out.println(i);                          
  }
}

public void countUp(int num) {
  int count = 1;
  for (int i = 0; i < num * 2; i+=2) {    
      System.out.println(count++);                          
  }
}

public void countUp(int num) {
  int count = 1;
  int upper = num * 2;
  for (int i = 1; i <= upper; i+=2) {    
      System.out.println(count++);                          
  }
}

The three programs above are doing the same thing (printing out numbers from $1$ to $N$ where $N$ is the value of num). The running time of all three will be in the form of a first-degree polynomial $T(N) = aN + b$ where the coefficients $a$ and $b$ are going to be different for each program.

So, the coefficients (constant factors) depend on how we express an algorithm (i.e., the programming language used to implement the algorithm, the compiler which converts the program to machine instructions, the Instruction Set Architecture of the hardware it will eventually run on, etc.) To normalize this variation, we can drop the constants (set them to $1$), effectively considering $T(N) \propto n^{2} + n + \lg n + 1$.

Moreover, when the input gets larger and larger, the highest-order term, $n^{2}$ is going to be much much larger than all the lower-order terms combined (i.e. $n + \lg n + 1$). So, when the input gets large, the performance really comes down to the dominant term.

Why does the dominant term dictate the performance?

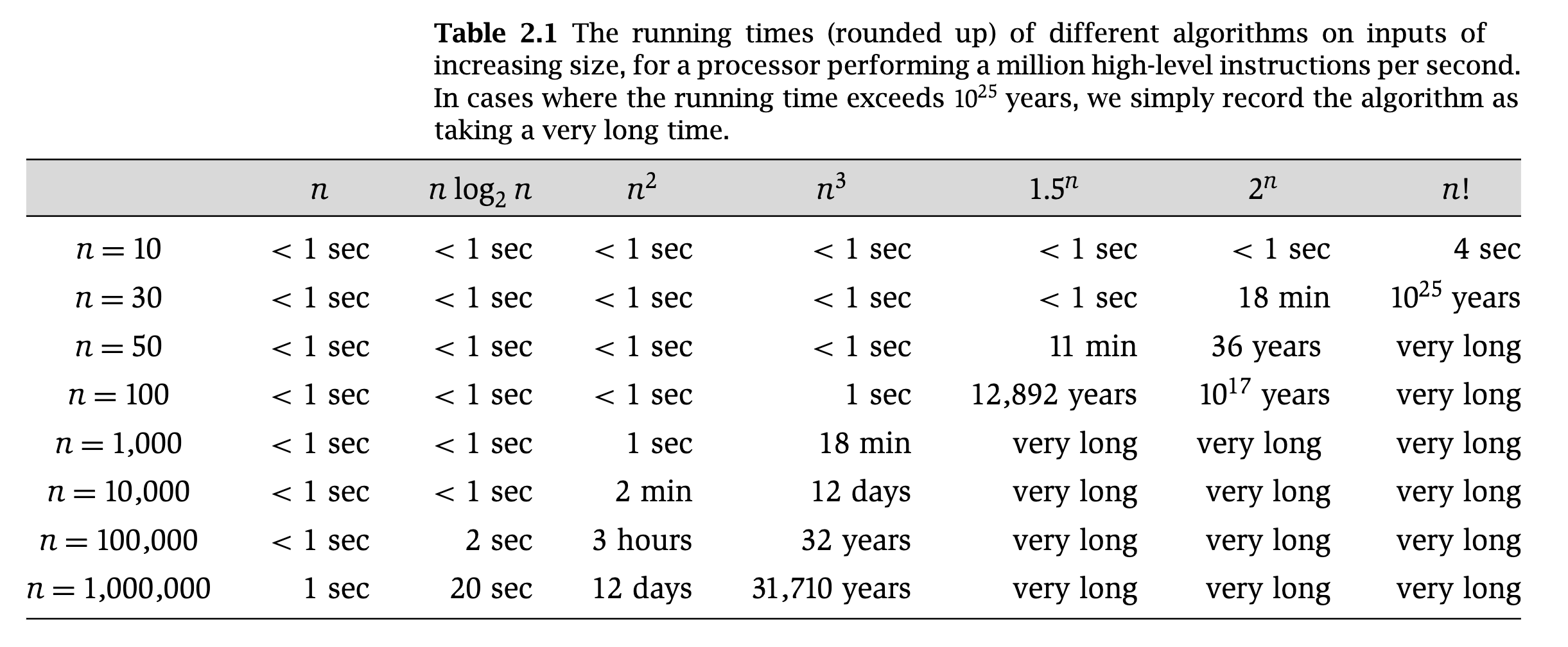
The following table is from the book "Algorithm design" by Jon Kleinberg and Eva Tardos (2006). You can see how different functions' runtime grows with increasing the input size.