Treap Deletion: Exercise
Consider the following (max-heap) treap, where the keys are the letters and the priorities are the integers:
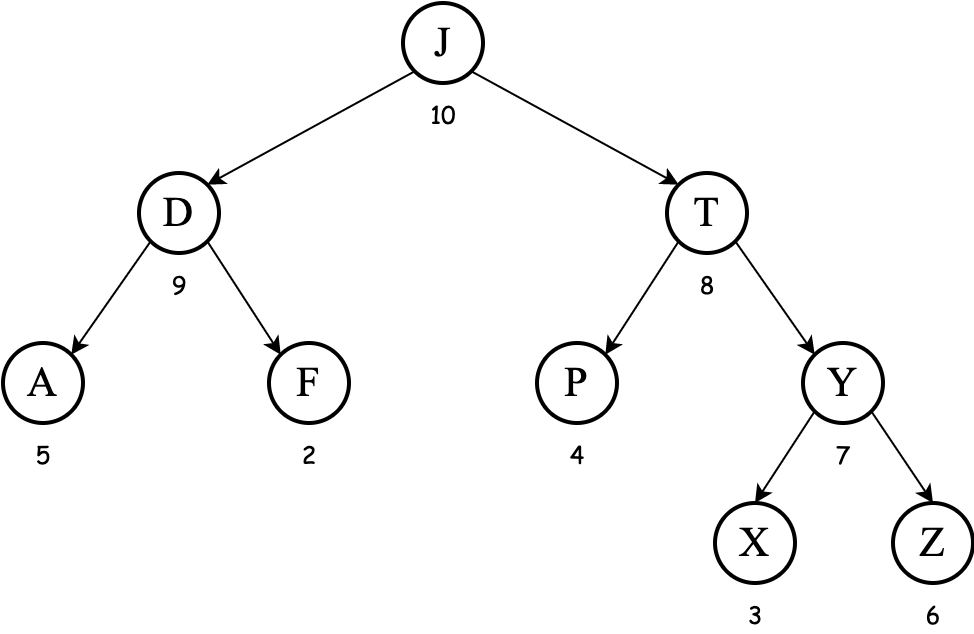
Exercise Show the result of removing the key T, including any necessary rotations.
Solution
After finding node with key T we set its priority to $-1$:
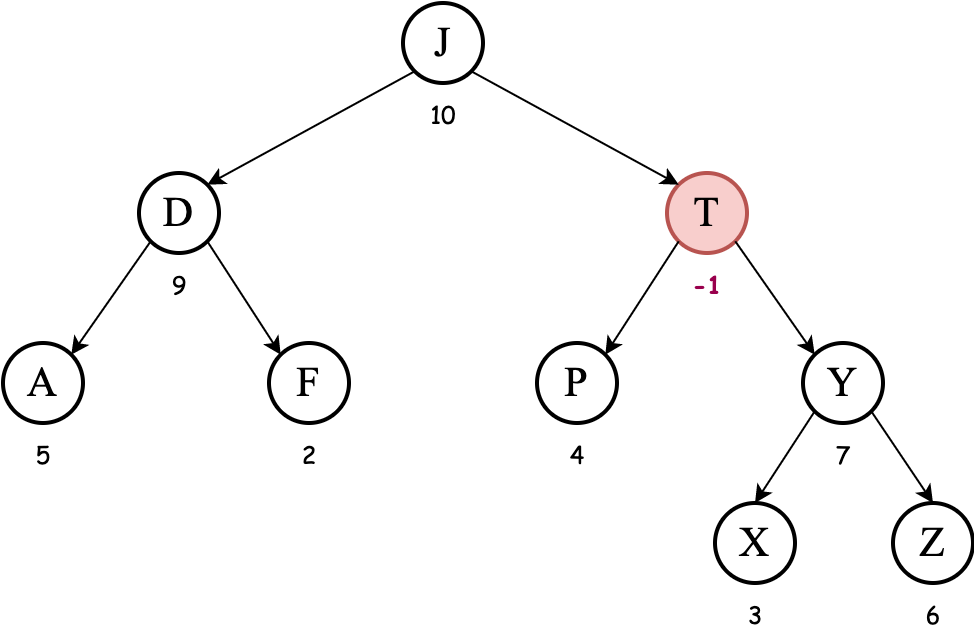
We must now apply tree rotations to fix the max-heap order property. Among the children of T, the node with key Y has the highest priority. So we must apply a left rotation to bring Y above T:
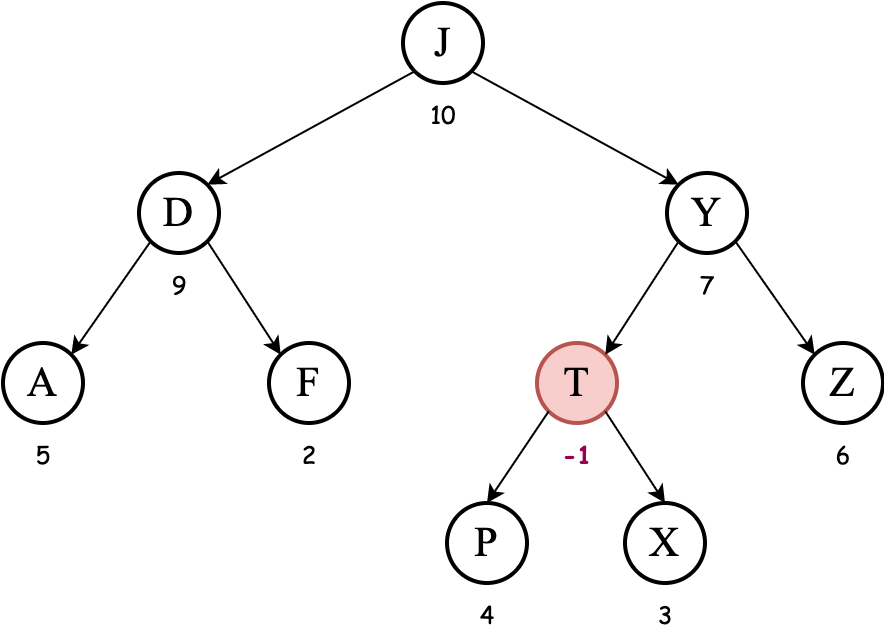
Among the children of T, the node with key P has the highest priority. So we must apply a right rotation to bring P above T:

Notice at this point we can simply remove T (since it has only one child). If we were to follow the process completely, we would have to apply another left rotation to bring X above T:
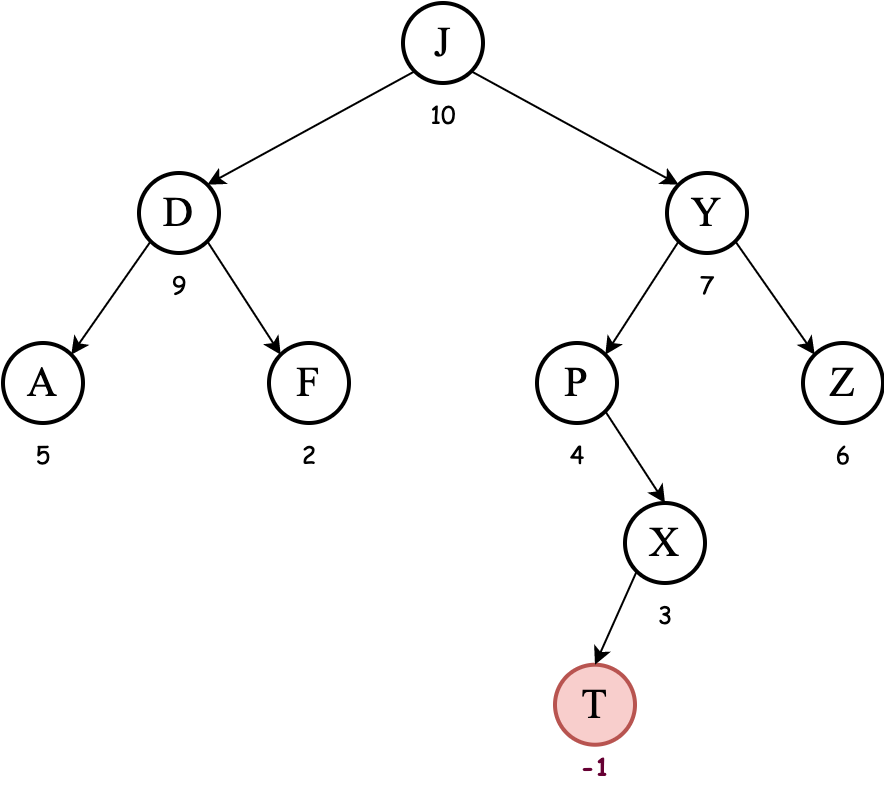
Now the node with key $T$ is a leaf, we will remove it!
